《线性代数》课程教学资源（讲稿B，高教版）第一章 矩阵及其初等变换 1-2 高斯消元法和矩阵的初等变换

1-2高斯消元法与矩车的初等变换一、高斯消元法二、矩阵的初等变换三、初等矩阵

1-2 高斯消元法与矩阵的初等变换 一、高斯消元法 二、矩阵的初等变换 三、初等矩阵

一、高斯消元法[3x, - x +5x3 =31引例X - x2 +2x =1用消元法解线性方程组X-2x2—X3=2③X -2x2 - x = 2X -2x2 - x = 2Xi-2x2 - x =2③-5②②-1X2 +3x3 = -1X - x+2x =1X, +3x, =-1③-305x2 +8x, =-3-7x, = 23x-X2+5x=310x =7X-2x- x= 21方程组的解为X2 +3x = -1X2 =722X3 =7X3=7

一、高斯消元法 引例 用消元法解线性方程组               2 2 2 1 3 5 3 1 2 3 1 2 3 1 2 3 x x x x x x x x x ① ② ③               3 5 3 2 1 2 2 1 2 3 1 2 3 1 2 3 x x x x x x x x x ①←→③ ②-① ③-3①               5 8 3 3 1 2 2 2 3 2 3 1 2 3 x x x x x x x              7 2 3 1 2 2 3 2 3 1 2 3 x x x x x x ③-5② ③         7 1                7 2 3 1 2 2 3 2 3 1 2 3 x x x x x x 方程组的解为               7 2 7 1 7 10 3 2 1 x x x

?X+3x2+4x=0再看一例22x +5x2 + 9x =03x, +7x2 +14x = 0X2- Xg= 04X+3x2+4x=0X+3x2+4x3=01+3x2+4x=0②-2@③-2@-X+ =0-X+ X= 0X2-x=0@-30④+②0=0-2x +2x, = 00=0X2- x=0X, =-7xX2=X3

再看一例             0 3 7 14 0 2 5 9 0 3 4 0 2 3 1 2 3 1 2 3 1 2 3 x x x x x x x x x x x ①②③④ ② - 2 ① ③ - 3 ①             0 2 2 0 0 3 4 0 2 3 2 3 2 3 1 2 3 x x x x x x x x x ③ - 2 ② ④ + ②         0 0 0 0 0 3 4 0 2 3 1 2 3 x x x x x       0 3 4 0 2 3 1 2 3 x x x x x    2 3 1 3 7 x x x x

ax+ai2x+...+anx,=b线性方程组的初等变换a2ixj+a22x2+...+a2nx,=b,amXj+am2X2+...+ammx,=b线性方程组的消元法，把方程组化为同解方程组，变换可归结为以下三种形式（1）交换两个方程的位置；（2）用一个非零常数乘某个方程；（3）用一个非零常数乘某个方程然后加到另一个方程

线性方程组的消元法，把方程组化为同解方程组，变换可归结为以下三种形式： （1）交换两个方程的位置； （2）用一个非零常数乘某个方程； （3）用一个非零常数乘某个方程然后加到另一个方程。 线性方程组的初等变换                    m m mn n m n n n n a x a x a x b a x a x a x b a x a x a x b     1 1 2 2 2 1 1 2 2 2 2 2 1 1 1 1 2 2 1 1

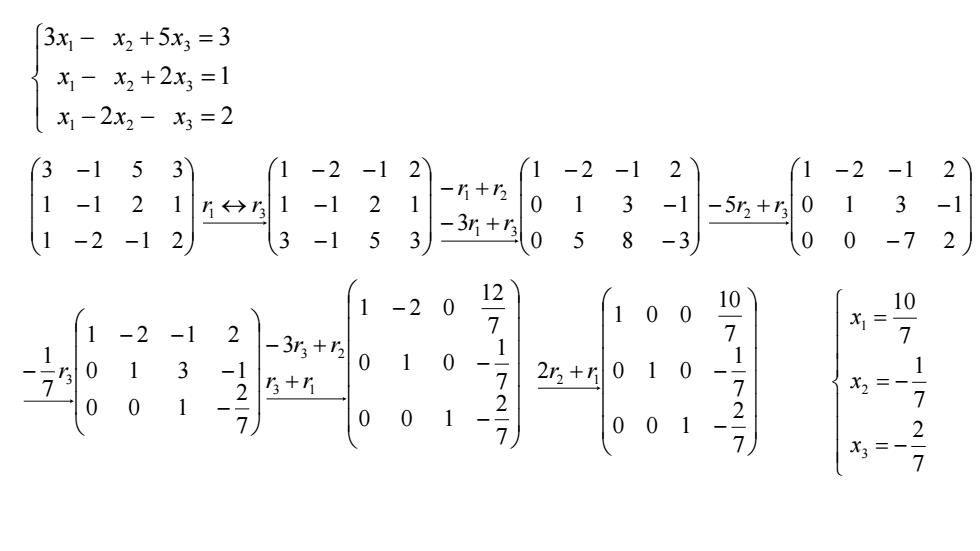
3x-X2+5x3=3X - x2 +2x; =1X-2x2 - g=2(33)5-1(122(12-2-1-2-1-11-2-r+r112033-1215r, +r0111-1-1-1rr-3r+r30(152,-2(3508-3)(0-7-12)-11210101-20C7XI=77-2-1213r+r1010131-12r, +1177r+rX2=27020120700277X3=7

              2 2 2 1 3 5 3 1 2 3 1 2 3 1 2 3 x x x x x x x x x               1 2 1 2 1 1 2 1 3 1 5 3               7 2 7 1 7 10 3 2 1 x x x                3 1 5 3 1 1 2 1 1 2 1 2 1 3 r r                   0 5 8 3 0 1 3 1 1 2 1 2 3 1 3 1 2 r r r r                 0 0 7 2 0 1 3 1 1 2 1 2 5 2 3 r r                  7 2 0 0 1 0 1 3 1 1 2 1 2 7 1 3 r                       7 2 0 0 1 7 1 0 1 0 7 12 1 2 0 3 3 1 3 2 r r r r                    7 2 0 0 1 7 1 0 1 0 7 10 1 0 0 2 2 1 r r