
线性代数敖程 第一章阶行列式 第五节 阶行列式的性质 一、行列式的性质 二、应用举例 三、小结、思考题
线性代数教程 线性代数小组 第一章 n阶行列式 第五 节 阶行列式的性质 一、行列式的性质 三、小结、思考题 二、应用举例
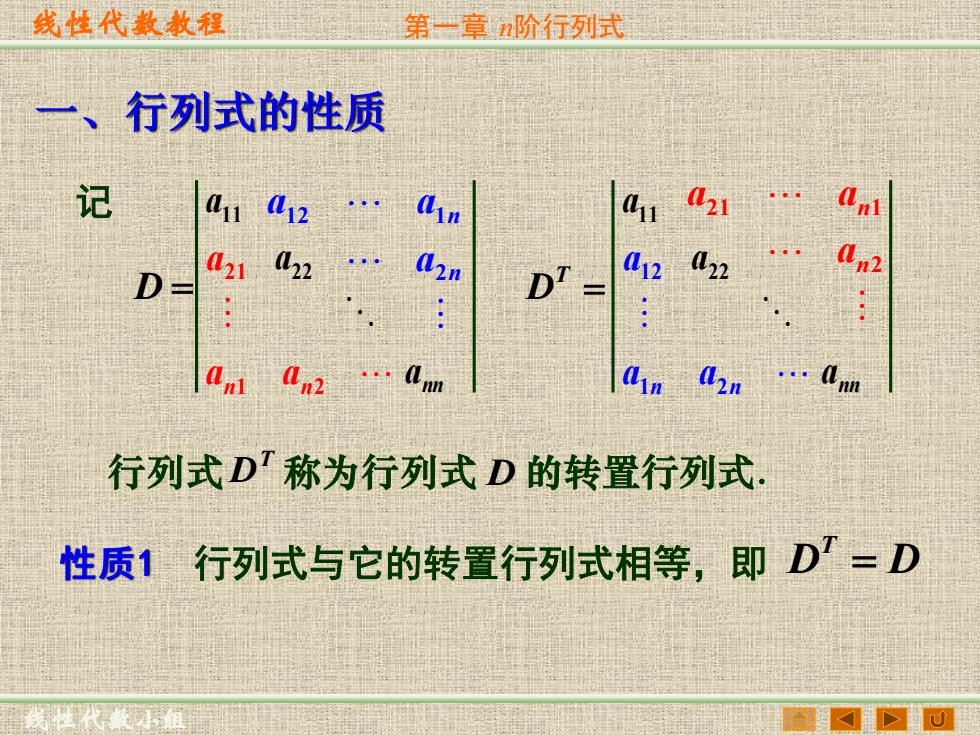
线性代数教程 第一章阶行列式 一、行列式的性质 记 411412 411 421. D里 021022 a2n DT= 012 (l22 2m 凸1n Q2n .lm 行列式D'称为行列式D的转置行列式 性质1 行列式与它的转置行列式相等,即D'=D
线性代数教程 线性代数小组 第一章 n阶行列式 一、行列式的性质 行列式 称为行列式 的转置行列式. T D D 记 nn a a a 22 11 n n a a a 2 12 1 1 2 21 n n a a a D = 2 21 1 n n a a a n n a a a 1 2 12 = T D nn a a a 22 11 性质1 行列式与它的转置行列式相等,即 T D D=

线性代数故程 第一章阶行列式 证明记D=deta,的转置行列式 b11b 2.b1n DT= 1b22.b2n . bat Bn2 bun 即b,=a,(6j=1,2,n),按定义 D'=∑(T.-∑anaw20n 又因为行列式D可表示为 D=∑(-1y0n0p2apn
线性代数教程 线性代数小组 第一章 n阶行列式 证明 记 D = det(aij)的转置行列式, 1 2 2 1 2 2 2 1 1 1 2 1 n n nn n n T b b b b b b b b b D = b a (i, j 1,2, ,n), 即 ij = ij = 按定义 ( 1) ( 1) . = − 1 1 2 2 = − p11 p2 2 p n t p p np T t n n D b b b a a a 又因为行列式D可表示为 ( 1) . = − p11 p2 2 p n t n D a a a

线性代教教程 第一章阶行列式 故 D=DT 证毕 说明行列式中行与列具有同等的地位,因此行列 式的性质凡是对行成立的对列也同样成立. 性质2 互换行列式的两行(列),行列式变号 证明 设行列式 b b12 D1= b21b22 .b2m Bat Bn2 ban 是由行列式D=deta,)变换i,j两行得到的
线性代数教程 线性代数小组 第一章 n阶行列式 故 . T D = D 证毕 性质2 互换行列式的两行(列),行列式变号. 证明 设行列式 , 1 2 2 1 2 2 2 1 1 1 2 1 1 n n nn n n b b b b b b b b b D = 说明 行列式中行与列具有同等的地位,因此行列 式的性质凡是对行成立的对列也同样成立. 是由行列式 D = det(aij) 变换 两行得到的, i, j

线性代数教程 第一章阶行列式 即当k≠i,j时,bo=ap当k=i,j时, bp-ai'bin ap 于是 D=∑(bnb%bm,bm =∑(-yan.0p0n =∑(1yanp0nm. 其中1.i.j.n为自然排列, 伪排列p,p.P.pn的逆序数 设排列p1.pp,.Pn的逆序数为,则有
线性代数教程 线性代数小组 第一章 n阶行列式 于是 ( ) i j npn p ip jp t D b b b b 1 1 1 = − 1 ( ) i j npn p ip jp t a a a a 1 1 = − 1 ( 1) , 1 1 j i npn p ip jp t = − a a a a 其中1i jn为自然排列, . t为排列 p1 pi pj pn 的逆序数 , 1 1 p p p p t 设排列 i j n 的逆序数为 则有 即当 时, k i, j ; bkp = akp 当 k i j 时, = , , , bip = ajp bjp = aip