
线性代数敖程 第-章阶行列式 第二节 全排列及其逆序数 一、概念的引入 二、全排列及其逆序数 三、小结
线性代数教程 线性代数小组 第一章 n阶行列式 第二 节 全排列及其逆序数 一、概念的引入 三、小结 二、全排列及其逆序数

线性代数敖程 第一章阶行列式 一、概念的引入 引例用1、2、3三个数字,可以组成多少个没 有重复数字的三位数? 解 123 百位 3 3种放法 十位 2 2种放法 个位12 1种放法 共有3×2×1=6种放法
线性代数教程 线性代数小组 第一章 n阶行列式 一、概念的引入 引例 用1、2、3三个数字,可以组成多少个没 有重复数字的三位数? 解 1 2 3 百位 1 2 3 3种放法 十位 1 2 1 3 个位 1 2 3 2种放法 1种放法 共有 3 21 = 6 种放法

线性代教教程 第一章阶行列式 二、全排列及其逆序数 问题把n个不同的元素排成一列,共有几种不 同的排法? 定义 把n个不同的元素排成一列,叫做这n个 元素的全排列(或排列), n个不同的元素的所有排列的种数,通常 用Pn表示 结论:n个元素的全排列共有n!个 nx(n-1)×(n-2)×.×2×1=n!
线性代数教程 线性代数小组 第一章 n阶行列式 二、全排列及其逆序数 同的排法? 问题 把 n 个不同的元素排成一列,共有几种不 定义 把 个不同的元素排成一列,叫做这 个 元素的全排列(或排列). n n 个不同的元素的所有排列的种数,通常 用 表示. n Pn 结论:n个元素的全排列共有 n!个 . n n n n − − = ( 1) ( 2) 2 1 !
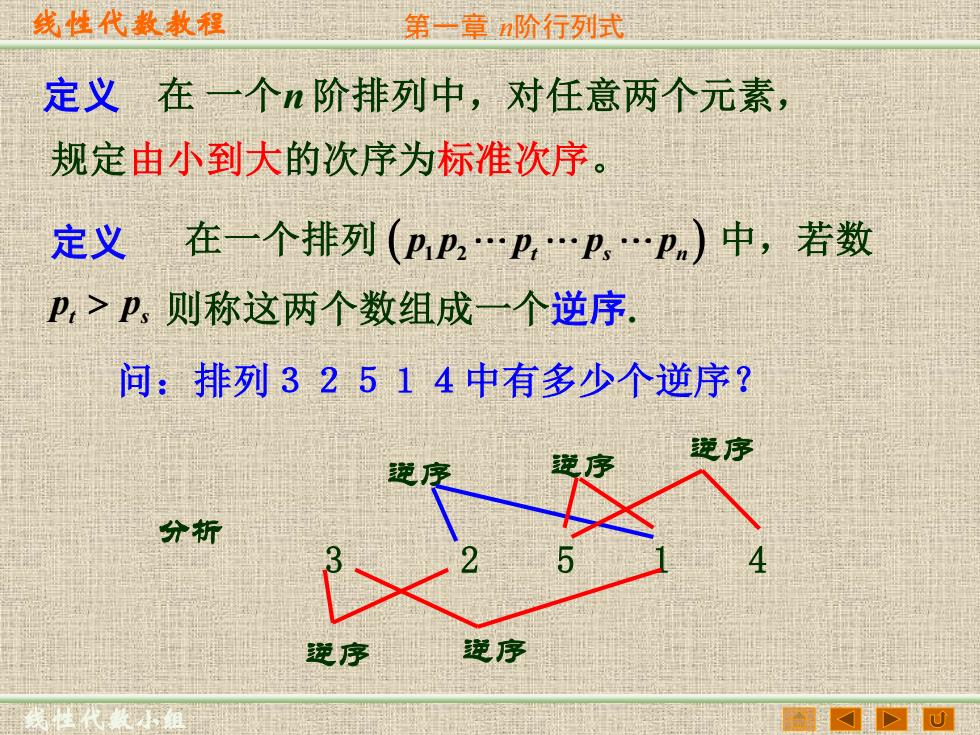
线性代数敖程 第一章阶行列武 定义在一个n阶排列中,对任意两个元素, 规定由小到大的次序为标准次序。 定义在一个排列(pP2.2,.p,.P)中,若数 卫,>P,则称这两个数组成一个逆序 问:排列32514中有多少个逆序? 逆序 逆序 分析 逆序 逆序
线性代数教程 线性代数小组 第一章 n阶行列式 定义 在 一个n 阶排列中,对任意两个元素, 规定由小到大的次序为标准次序。 在一个排列 中,若数 则称这两个数组成一个逆序. ( p p p p p 1 2 t s n ) t s p p 定义 问:排列32514中有多少个逆序? 3 2 5 1 4 逆序 逆序 逆序 逆序 分析 逆序

线性代数教程 第一章阶行列式 排列的逆序数 一个排列中所有逆序的总数,称为这个排列 的逆序数,记为:tor.t(pP.P) 排列的奇偶性 逆序数为奇数的排列称为奇排列; 逆序数为偶数的排列称为偶排列, 逆序数为0的排列,称为标准排列
线性代数教程 线性代数小组 第一章 n阶行列式 一个排列中所有逆序的总数, 的逆序数, 称为这个排列 1 2 . . n 记为:t or (p p p ) 逆序数为奇数的排列称为奇排列; 逆序数为偶数的排列称为偶排列. 排列的奇偶性 排列的逆序数 逆序数为0的排列,称为标准排列