
线性代教教程 第0101节二阶与三阶行列式 2345 第一节矩阵 一、矩阵概念的引入 二、矩阵的定义 三、小结 第页
线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:45 第1页 第一节 矩阵 一、矩阵概念的引入 三、小结 二、矩阵的定义

线性代数教程 第0101节三阶与三阶行列式 2345 一、矩阵概念的引入 4x,+02x2+.+4xn=b 1.线性方程组 021+02火2+.+02xn=b2 ax+ax+.+ax=b 的解取决于 系数0,j=12,n, 常数项b(=1,2,n) 第2项
线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:45 第2页 + + + = + + + = + + + = n n nn n n n n n n a x a x a x b a x a x a x b a x a x a x b 1 1 2 2 21 1 22 2 2 2 11 1 12 2 1 1 1. 线性方程组 的解取决于 a (i, j 1,2, ,n), 系数 ij = b (i n) i 常数项 = 1,2, , 一、矩阵概念的引入
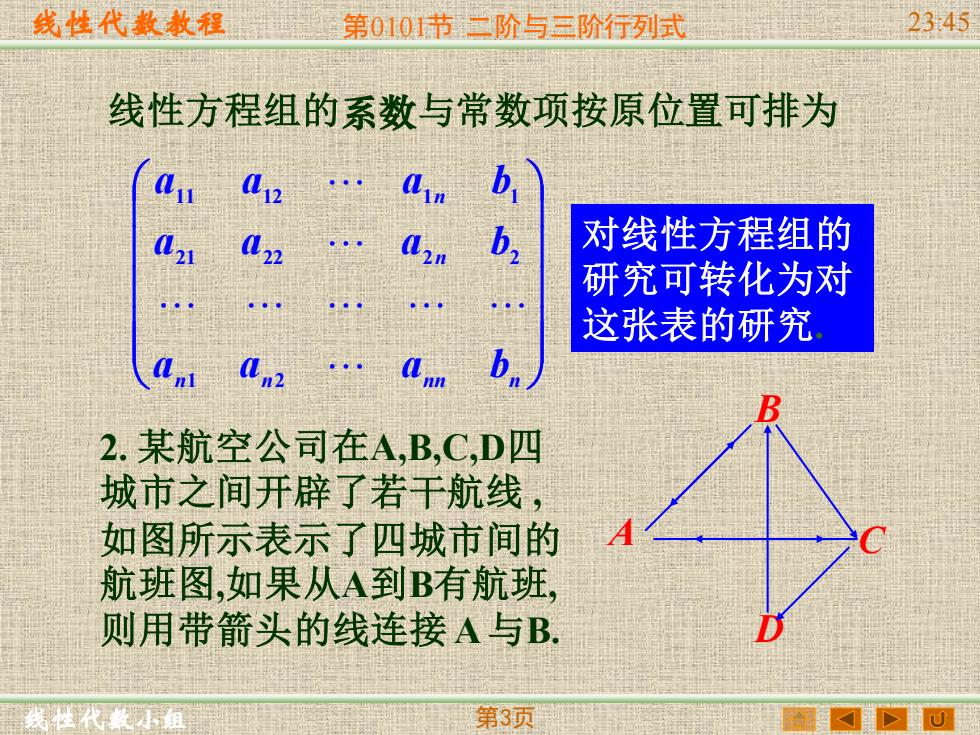
线性代数教程 第0101节二阶与三阶行列式 23.45 线性方程组的系数与常数项按原位置可排为 12 · L21 22 b 对线性方程组的 研究可转化为对 。 这张表的研究 ·0m 2.某航空公司在A,B,C,D四 城市之间开辟了若干航线, 如图所示表示了四城市间的 航班图,如果从A到B有航班, 则用带箭头的线连接A与B. 第3页
线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:45 第3页 n n nn n n n a a a b a a a b a a a b 1 2 21 22 2 2 11 12 1 1 对线性方程组的 研究可转化为对 这张表的研究. 线性方程组的系数与常数项按原位置可排为 2. 某航空公司在A,B,C,D四 城市之间开辟了若干航线 , 如图所示表示了四城市间的 航班图,如果从A到B有航班, 则用带箭头的线连接 A 与B. A B C D

线性代数赦程 第0101节三阶与三阶行列式 23:45 四城市间的航班图情况常用表格来表示: 到站 B B 发站 D 其中一表示有航班. 为了便于计算,把表中的八一改成1,空白地方填上 0,就得到一个数表: 第4项
线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:45 第4页 四城市间的航班图情况常用表格来表示: 发站 到站 A B C D A B C D 其中 表示有航班. 为了便于计算,把表中的 改成1,空白地方填上 0,就得到一个数表: A B C D
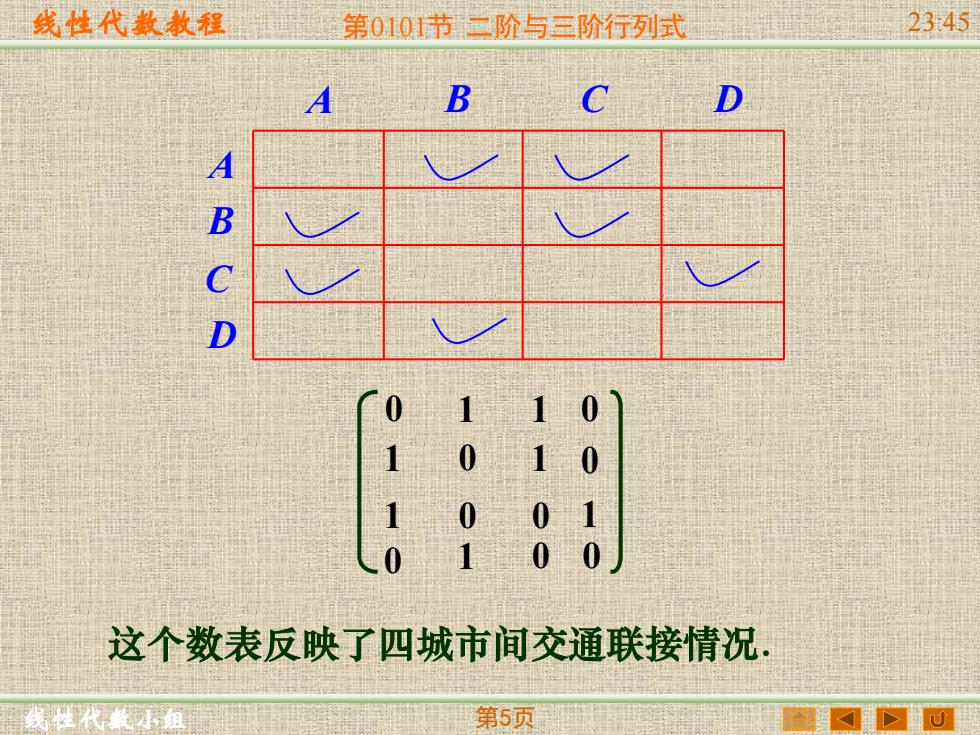
线性代数教程 第0101节二阶与三阶行列式 2345 B D ABCD 10 0 10 这个数表反映了四城市间交通联接情况. 第5页
线性代数教程 线性代数小组 第0101节 二阶与三阶行列式 23:45 第5页 这个数表反映了四城市间交通联接情况. A B C D A B C D 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0