
线性代教教程 第一章阶行列式 第四节对换 一、对换的定义 二、对换与排列的奇偶性的关系 三、小结、思考题
线性代数教程 线性代数小组 第一章 n阶行列式 第四节 对换 一、对换的定义 三、小结、思考题 二、对换与排列的奇偶性的关系
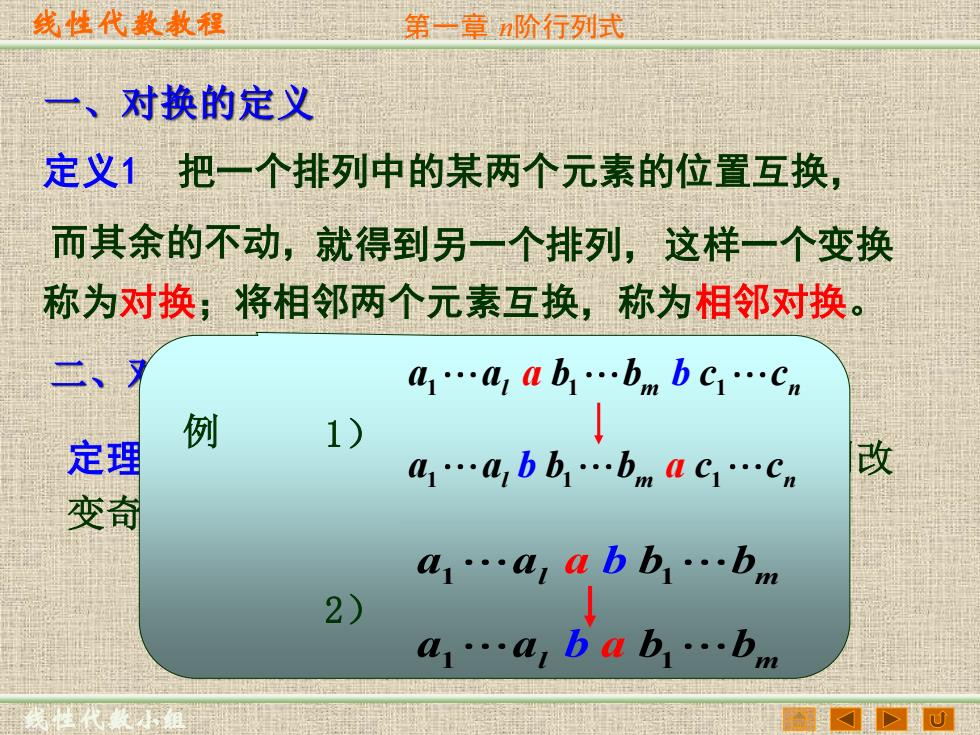
线性代数敖程 第一章阶行列式 一、对换的定义 定义1把一个排列中的某两个元素的位置互换, 而其余的不动,就得到另一个排列,这样一个变换 称为对换;将相邻两个元素互换,称为相邻对换。 二、习 a1.4,a b.ombc.c。 例 1) ↓ 定理 a1.4,bb.bmaC1.Cn 改 变奇 a1.a,abb1.bnm 2) a1.a1bab.b 回
线性代数教程 线性代数小组 第一章 n阶行列式 一、对换的定义 定义1 把一个排列中的某两个元素的位置互换, 而其余的不动,就得到另一个排列,这样一个变换 称为对换;将相邻两个元素互换,称为相邻对换。 二、对换与排列的奇偶性的关系 定理1 一个排列中的任意两个元素对换,排列改 变奇偶性。 a a b b 1 1 l m a b a a b b 1 1 l m b a 1 1 1 l m n a a b b c a b c 1 1 1 l m n a a b b c b a c 2) 例 1)

线性代数教程 第一章阶行列式 定理1一个排列中的任意两个元素对换,排列改 变奇偶性。 证明:设排列为2) 441b6-bn对换a,b a1.a,bab1-bm 易见除4,b外,其它元素的逆序数不改变, 若a>b 对换后的逆序数不变,而b的逆序数减1; 若a<b 对换后a的逆序数增1,而b的逆序数不变, 因此对换相邻两个元素,排列改变奇偶性
线性代数教程 线性代数小组 第一章 n阶行列式 1 1 l m a a b b a b 1 1 l m a a b b b a 定理1 一个排列中的任意两个元素对换,排列改 变奇偶性。 证明:设排列为 2) 易见除 a b, 外,其它元素的逆序数不改变, 若 a b 对换 a b, 对换后 a 的逆序数不变,而 b 的逆序数减1; 若 a b 对换后 a 的逆序数增1,而 b 的逆序数不变. 因此对换相邻两个元素,排列改变奇偶性
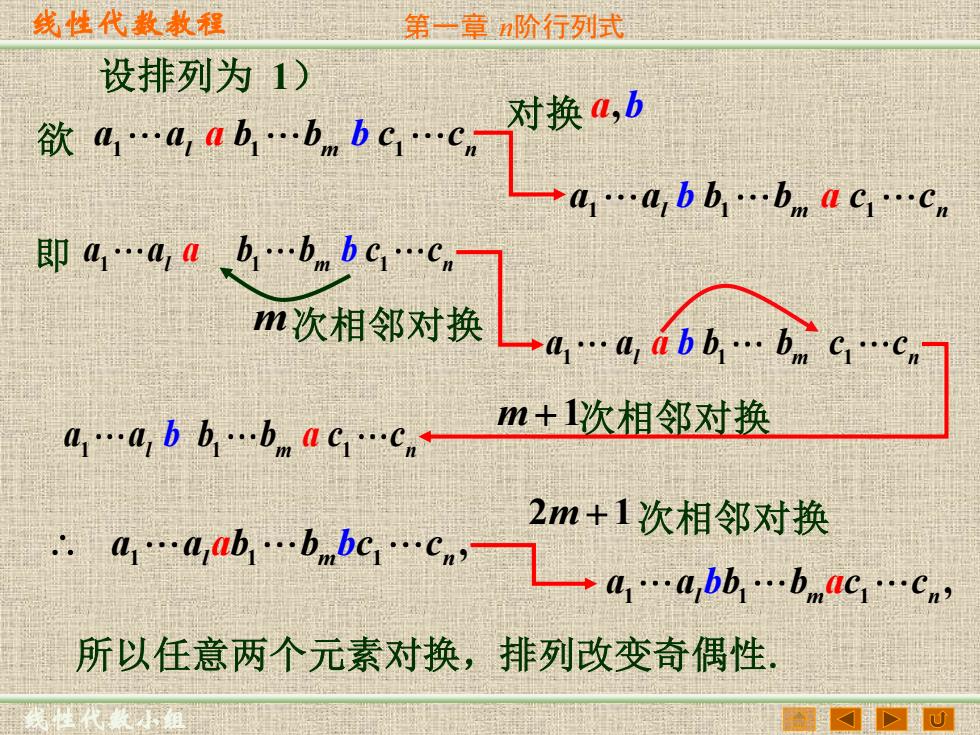
线性代款教程 第一章阶行列式 设排列为1) 欲40a而bnbc-C,对换h 一4.abh-bnaG.c。 即4.a10b.bnbc1.c. m次相邻对换4.ab669-c 0.4 bbbac.c m+1次相邻对换 A.4ahb.bc-C4.nb-b.Gc 2m+1次相邻对换 所以任意两个元素对换,排列改变奇偶性
线性代数教程 线性代数小组 第一章 n阶行列式 1 1 1 l m n a a b b c a b c 1 1 1 l m n a a b b c b a c 设排列为 1) 对换 a,b m 次相邻对换 1 1 1 l m n a a b b c a b c 1 1 1 , l m n a a b ab bc c 1 1 1 , l m n a a b b b ac c 所以任意两个元素对换,排列改变奇偶性. 1 1 1 l m n a a b b c a b c 1 1 1 l m n a a b b c b a c 2 1 m + 次相邻对换 欲 即 m + 1 次相邻对换

线性代数故程 第一章阶行列式 定理2 n个元素(n>1)共有n:个n阶排列,其中奇、 偶排列各占一半, 证明:设共有s个奇排列,1个偶排列,现证s=t, s个奇排列 前两个数对换 s个偶排列所以s≤t t个偶排列 前两个数对换 t个奇排列所以t≤s 故必有S=t
线性代数教程 线性代数小组 第一章 n阶行列式 定理2 n个元素(n >1)共有n!个n阶排列 , 其中奇、 偶排列各占一半. 证明: 设共有 s个奇排列, t 个偶排列,现证s=t. 故必有 s = t. 奇排列 偶排列 所以 s t 前两个数对换 s 个 s 个 t 个 偶排列 前两个数对换 t 个奇排列 所以 t s