
例2 求出函数 f(x)= x3 +3x2-24x-20的极值。解 f'(x) = 3x2 + 6x -24 = 3(x+ 4)(x -2)令 f(x)=0, 得驻点 xi =-4, x2 = 2.: f"(x) = 6x + 6,故极大值 f(-4)=60,: f"(-4) = -18<0.f"(2) = 18 > 0,故极小值f(2)=-48.f(x)=x3 +3x2-24x-20图形如下
例2 解 ( ) 3 24 20 . 求出函数 f x = x 3 + x 2 x − 的极值 ( ) 3 6 24 2 f x = x + x − 令 f (x) = 0, 4, 2. 得驻点 x1 = − x2 = = 3(x + 4)(x − 2) f (x) = 6x + 6, f (−4) = − 18 0, 故极大值 f (−4) = 60, f (2) = 18 0, 故极小值 f (2) = −48. ( ) 3 24 20 3 2 f x = x + x − x − 图形如下
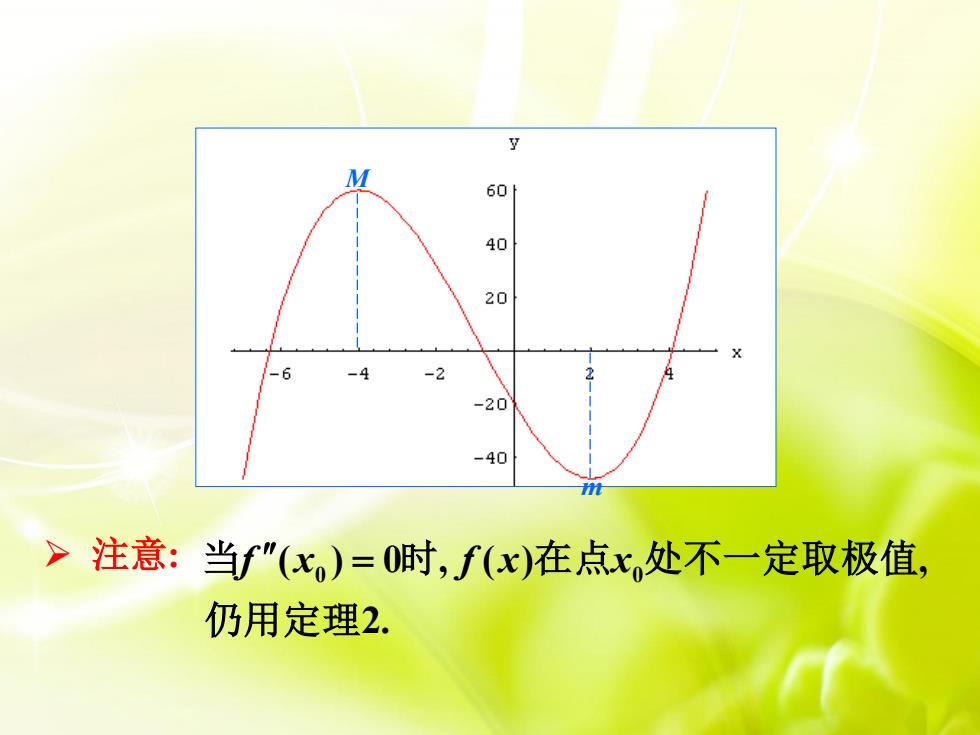
604020-6-4-2-20-40tmt注意:当f"(x)=0时,f(x)在点x,处不一定取极值仍用定理2
M m ➢ 注意: 0 0 ( ) 0 , ( ) , 2. 当f x f x x = 时 在点 处不一定取极值 仍用定理

例3 求函数f(x)=(x2-1)2+1的极值解: f'(x)=6x(x2-1)令f(x)=0,求得驻点x, =-1,x, = 0,x, =1.f"(x) = 6(x2 -1)(5x2 -1).因f"(0)=6>0,故f(x)在x =0处取得极小值,极小值为f(0)=0.因f"(-1)= f"(1)= 0,故用定理3无法判别考察一阶导数f(x)在驻点xj =-1,x, =1左右邻近的符号:
2 3 例3 ( ) ( 1) 1 求函数f x x = − + 的极值. 2 2 1 2 3 ( ) 6 ( 1) ( ) 0, 1, 0, 1. f x x x f x x x x 解: . 令 求得驻点 = − = = − = = 2 2 f x x x ( ) 6( 1)(5 1). = − − (0) 6 0 ( ) 0 (0) 0. f f x x f 因 ,故 在 处取得极小值, 极小值为 = = = 1 3 ( 1) (1) 0 3 ( ) 1, 1 f f f x x x 因 ,故用定理 无法判别. 考察一阶导数 在驻点 左 右邻近的符号: − = = = − =

当x取-1左侧邻近值时,f'(x)<0;当x取-1有侧邻近值时,f(x)<0;因为f(x)的符号没有改变,所以f(x)在x =-1处不取得极值.同理f(x)在x=1处也不取得极值+
1 x y −1 1 ( ) 0 1 ( ) 0 ( ) ( ) 1 ( ) 1 x f x x f x f x f x x f x x当 取 左侧邻近值时, ; 当 取 有侧邻近值时, ; 因为 的符号没有改变,所以 在 处不取得极值.同理 在 处也不取得极值. − − = − =

判别法的推广:若函数f(x)在x点有直到n阶导数:f'(x,)= f"(x,) =... = f(n-(x)= 0, f(n(x,)± 0则:(1)当n为偶数时,x,为极值点,且当f(n(x)>0时,x为极小值点;且当f(n(x)<0时,x,为极大值点;(2)当n为奇数时,x,不是极值点证:利用f(x)在x,点的泰勒公式可得(x-x)"-2f(x)= f(x)+ f'(x.)(x-x)+...+(n-1)!(5)(x-xo)"-1(n-1)!
0 ( 1) ( ) 0 0 0 0 ( ) ( ) ( ) ( ) 0, ( ) 0, n n f x x n f x f x f x f x − = = = = 判别法的推广:若函数 在 点有直到 阶导数, ( ) 0 0 ( ) 0 , ; n 且当f x x 时 为极小值点 0 则:(1)当n x 为偶数时, 为极值点, ( 2) 0 2 0 0 0 0 ( 1) 1 0 ( ) ( ) ( ) ( )( ) ( ) ( 1) ! ( ) ( ) ( 1) ! n n n n f x f x f x f x x x x x n f x x n − − − − = + − + + − − + − − 证: 0 利用f x x ( )在 点的泰勒公式可得 ( ) 0 0 ( ) 0 , ; n 且当f x x 时 为极大值点 0 (2)当n x 为奇数时, 不是极值点