yyoloXoxxXo(是极值点情形)y十十ofolxXoxXo(不是极值点情形)
x yo x y x0 o 0 x + − − + (是极值点情形) x y o 0 x + − + (不是极值点情形) 0 x − x y o

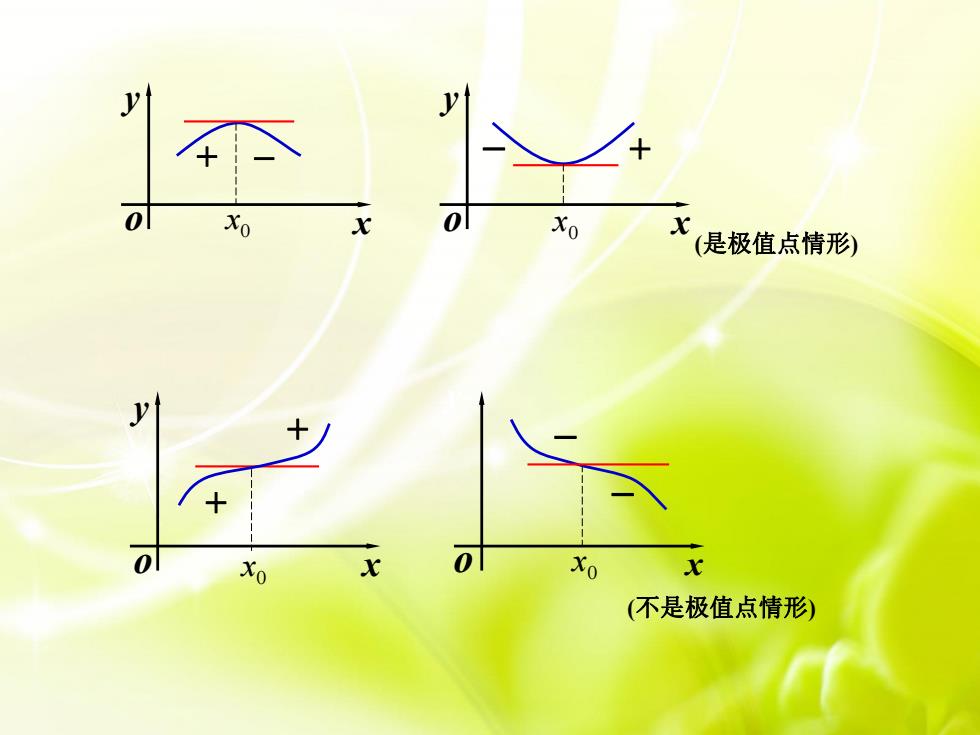
如果函数f(x)在所讨论的区间内连续,除个别点外处处可导求极值的步骤:(1)求导数 f(x);(2)求f(x)的驻点及不可导点;(3)考察f(x)在驻点及不可导点左右邻近的正负号,判断是否是极值点(4)求出极值
求极值的步骤: (1) 求导数 f (x); (2) ( ) ; 求f x 的驻点及不可导点 (3) ( ) , ; 考察 f x 在驻点及不可导点左右邻近 的正负号 判断是否是极值点 (4) . 求出极值 如果函数f(x)在所讨论的区间内连续,除个别点 外处处可导

例1 求函数f(x)=(x-4)/(x+1)的极值解:(1)f(x)在内(-80,+80)连续,除x=-1外处处可导,且5(x -1)f'(x) = 3/x+1(2)令f(x)=0,得驻点x =1,x=-1为f(x)的不可导点;(3)在(-80,-1)内,f'(x)>0;在(-1,1)内,f'(x)<0;故不可导点x =-1是一个极大值点;又在(1,+8o)内,f(x)>0,故驻点x=1是一个极小值点;
3 2 例1 ( ) ( 4) ( 1) 求函数f x x x = − + 的极值. 3 (1) ( ) ( , ) 1 5( 1) ( ) 3 1 f x x x f x x − + = − − = + 解: 在内 连续,除 外 处 可导,且 (2) ( ) 0 1 1 ( ) ; 令f x x x f x = = = − ,得驻点 , 为 的 不可导点 (3) ( , 1) ( ) 0; ( 1,1) ( ) 0; 1 (1, ) ( ) 0, 1 f x f x x f x x − − − = − + = 在 内, 在 内, 故不可导点 是一个极大值点;又在 内, 故驻点 是一个极小值点;
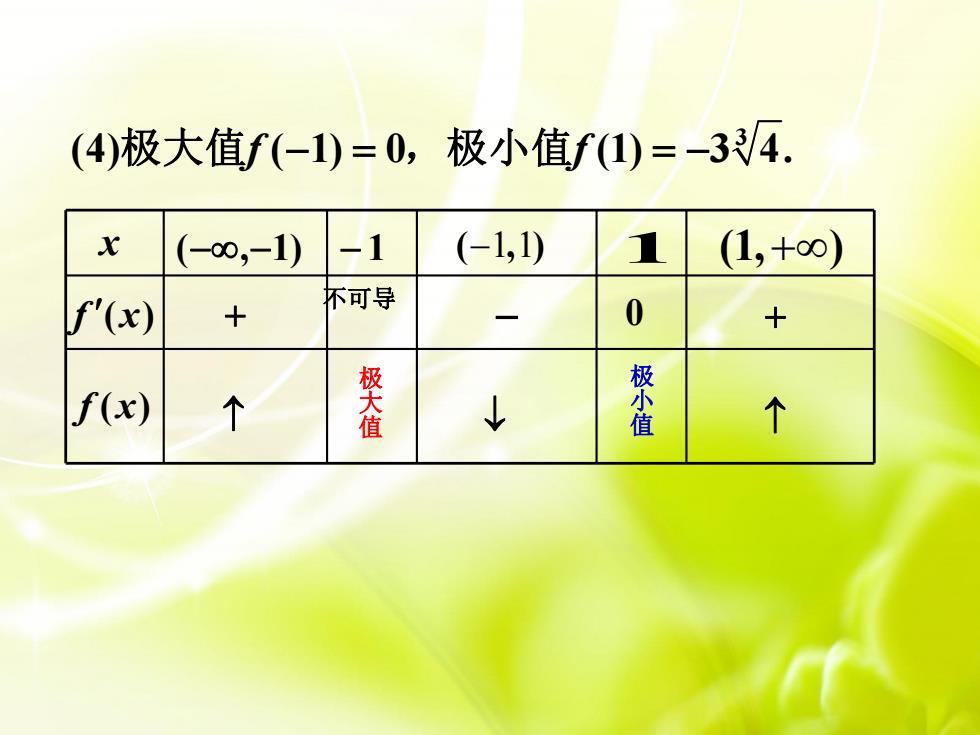
(4)极大值f(-1)=0,极小值f(1)=-3/4.x(-1, 1)(1, +8)-11(-80,-1)不可导0f'(x)++极小值极大值f(x)个个
3 (4) ( 1) 0 (1) 3 4. 极大值f f − = = − ,极小值 x (−,−1) − 1 ( , ) −1 1 1 (1, ) + f (x) f (x) + − + 0 极大值 极小值 不可导

设函数f(x)在x,处具有二阶导定理3(第二充分条件)1数,且f'(x)=0,f"(x)0,那么(1)当f"(x)<0时,函数f(x)在x处取得极大值;(2)当f"(x)>0时,函数f(x)在x,处取得极小值f'(x, +Ax)- f'(xo)<0证(I) : f"(xo)= lim =Ax4r-0故f'(x+△x)-f'(x)与△x异号,当△x<0时, 有f'(x +△x)>f'(x)= 0,当△x >0时,有f(x, +△x)< f'(x,)= 0,所以,函数f(x)在x,处取得极大值.同理可证(2)
证 (1) 0 0 0 0 ( ) ( ) ( ) lim 0, x f x x f x f x → x + − = 故f (x0 + x) − f (x0 )与x异号, 当x 0时, 0 0 有f x x f x ( ) ( ) 0, + = 当x 0时, 0 0 有f x x f x ( ) ( ) 0, + = 所以,函数 f (x)在x0处取得极大值. 同理可证(2). 0 0 0 0 0 0 0 ( ) ( ) 0 ( ) 0 (1) ( ) 0 ( ) (2) ( ) 0 ( ) . 3( ) f x x f x f x f x f x x f x f x x = 设函数 在 处具有二阶导 数,且 , ,那么 当 时,函数 在 处取得极大值; 当 时,函数 在 处 定理 第二充分条件 取得极小值