
高等数学 主计 本堂 第五章定积分 第一节 定积分的概念与性质 第二节 微积分基本公式 第三节 定积分的换元法和分部积分法 第四节 反常积分
山东农业大学 高等数学 主讲人:苏本堂 第五章 定积分 第一节 定积分的概念与性质 第二节 微积分基本公式 第三节 定积分的换元法和分部积分法 第四节 反常积分

第一节 定积分的概念与性质 一、定积分问题举例 二、定积分的定义 三、定积分的性质
山东农业大学 高等数学 主讲人:苏本堂 第一节 定积分的概念与性质 三、定积分的性质 一、定积分问题举例 二、定积分的定义
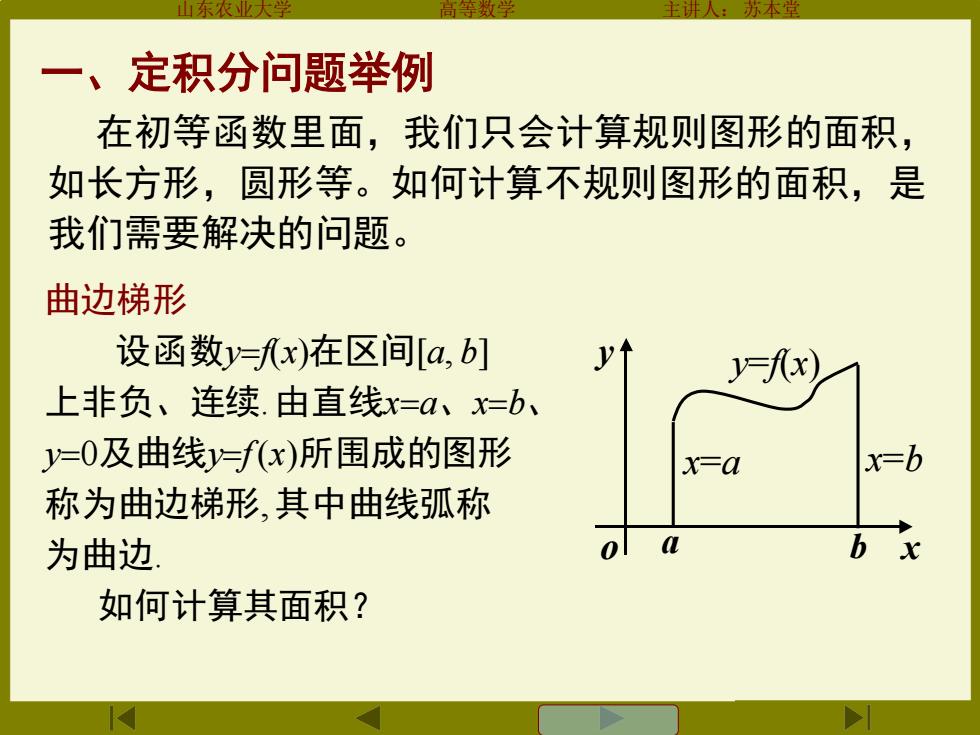
一、定积分问题举例 在初等函数里面,我们只会计算规则图形的面积, 如长方形,圆形等。如何计算不规则图形的面积,是 我们需要解决的问题。 曲边梯形 设函数y=x)在区间[a,b] =孔x) 上非负、连续.由直线x=a、x=b、 y=O及曲线y=fx)所围成的图形 x-a x=b 称为曲边梯形,其中曲线弧称 为曲边 0 L b 如何计算其面积?
山东农业大学 高等数学 主讲人:苏本堂 一、定积分问题举例 曲边梯形 设函数y=f(x)在区间[a, b] 上非负、连续. 由直线x=a、x=b、 y=0及曲线y=f(x)所围成的图形 称为曲边梯形, 其中曲线弧称 为曲边. 如何计算其面积? a b x y o y=f(x) x=a x=b 在初等函数里面,我们只会计算规则图形的面积, 如长方形,圆形等。如何计算不规则图形的面积,是 我们需要解决的问题

解决步骤: 1)分割. 在区间[a,b]中任意插入n-1个分点 a=0<1<x2<<xn-1<Xn=b 用直线x=x;将曲边梯形分成n个小曲边梯形, 2)近似.在第i个窄曲边梯形上任取5:∈[x;-1,x;] 1 作以[x-1,x]为底,f(5) 为高的小矩形,并以此小 梯形面积近似代替相应 窄曲边梯形面积△A,得 a x xXi-1xi bx 51 △4≈f(5i)△xi(Axi=x-x-1),i=1,2,.,n)
山东农业大学 高等数学 主讲人:苏本堂 1 x i x i−1 a x y o 解决步骤 : 1) 分割. 在区间 [a , b] 中任意插入 n –1 个分点 a = x0 x1 x2 xn−1 xn = b [ , ] i i 1 i x x − 用直线 i x = x 将曲边梯形分成 n 个小曲边梯形; 2) 近似. 在第i 个窄曲边梯形上任取 作以 [ , ] i 1 i x x − 为底 , ( )i f 为高的小矩形, 并以此小 梯形面积近似代替相应 窄曲边梯形面积 得 ( ) ( ) i i i i = i − i−1 A f x x x x i
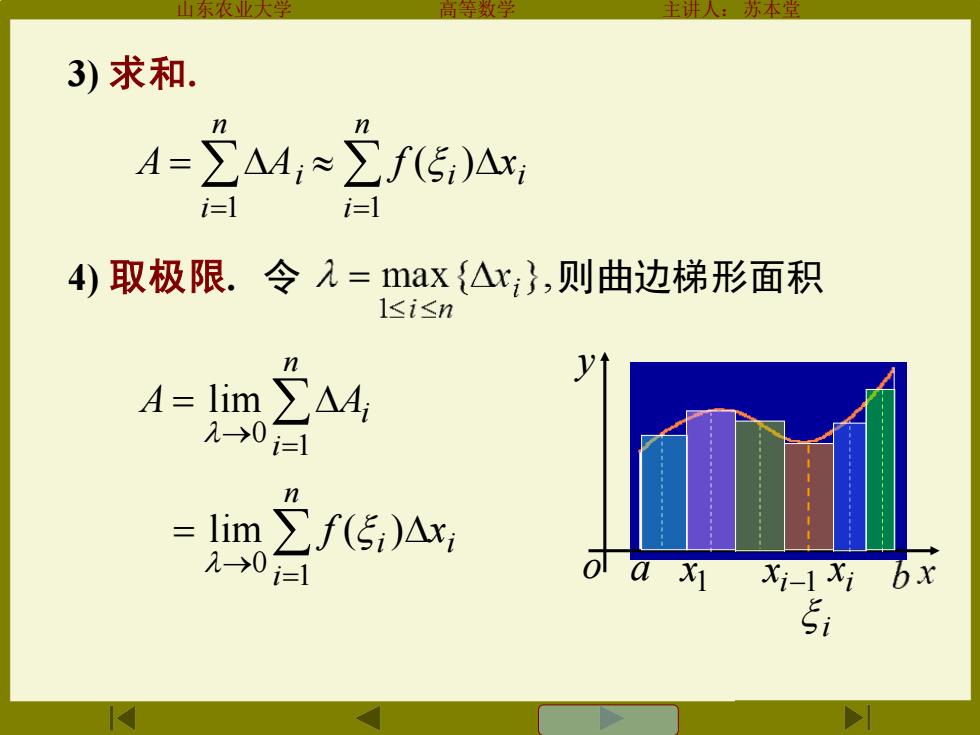
主讲 苏本堂 3)求和. A=∑A4,≈∑f(5:)△x 1 i=l 4)取极限.令元=max{△r;},则曲边梯形面积 l≤i≤n n A=lim∑A4, 1→01 = lim ∑f(5i)Ax: 201 Xi-1xi bx
山东农业大学 高等数学 主讲人:苏本堂 3) 求和. = = n i A Ai 1 = n i i i f x 1 ( ) 4) 取极限. 令 则曲边梯形面积 → = = n i A Ai 1 0 lim → = = n i i i f x 1 0 lim ( ) a y o 1 x i x i−1 x i