
主计 本 第三节泰勒公式 一、泰勒公式的建立 二、几个初等函数的麦克劳林公式 三、泰勒公式的应用
山东农业大学 高等数学 主讲人:苏本堂 第三节 泰勒公式 一、泰勒公式的建立 二、几个初等函数的麦克劳林公式 三、泰勒公式的应用

、泰勒公式的建立 1.问题的提出 根据函数的微分,有 x)=孔x+f'(xox-x)+o(x-x(当x-xo很小时), 略掉o(x-xo),得到求孔x)的近似公式 x)xo+f'(x)x-xo)(当x-xo很小时) 其误差为 R(xAx)Ax)f(xo)(-xo) 近似公式的不足:精确度不高,误差难于估计 为了达到一定的精确度要求,可考虑用n次多项式 Pnx)来近似表达x)
山东农业大学 高等数学 主讲人:苏本堂 一、泰勒公式的建立 1.问题的提出 根据函数的微分, 有 f(x)=f(x0 )+f (x0 )(x-x0 )+o(x-x0 )(当|x-x0 |很小时), 略掉o(x-x0 ), 得到求f(x)的近似公式 f(x)f(x0 )+f (x0 )(x-x0 )(当|x-x0 |很小时), 其误差为 R(x)=f(x)-f(x0 )-f (x0 )(x-x0 ). 近似公式的不足: 精确度不高, 误差难于估计. 为了达到一定的精确度要求, 可考虑用n次多项式 Pn (x)来近似表达f(x)

2.系数的确定 设函数x)在含x的开区间内具有直到(n+1)阶导数, 我们希望找出一个关于(x-xo)的n次多项式 Pn(x)=ao+a1(Gx-xota2(x-xo)2+·+an(x-xo” 来近似表达x).我们自然希望P(x)与x)在x的各阶导数 (直到(+1)阶导数)相等: Axo)=Pn(xo), f(o)=P(O). f"(o)=P"(o), f"(o)=Pn(o) f((xo)-P,()(xo)
山东农业大学 高等数学 主讲人:苏本堂 2.系数的确定 设函数f(x)在含x0的开区间内具有直到(n+1)阶导数, 我们希望找出一个关于(x−x0 )的n次多项式 Pn (x)=a0+a1 (x−x0 )+a2 (x−x0 ) 2+ +an (x−x0 ) n 来近似表达f(x). 我们自然希望Pn (x)与f(x)在x0的各阶导数 (直到(n+1)阶导数)相等: f(x0 )=Pn (x0 ), f (x0 )=Pn (x0 ), f (x0 )=Pn (x0 ), f (x0 )=Pn (x0 ), , f (n) (x0 )=Pn (n) (x0 )
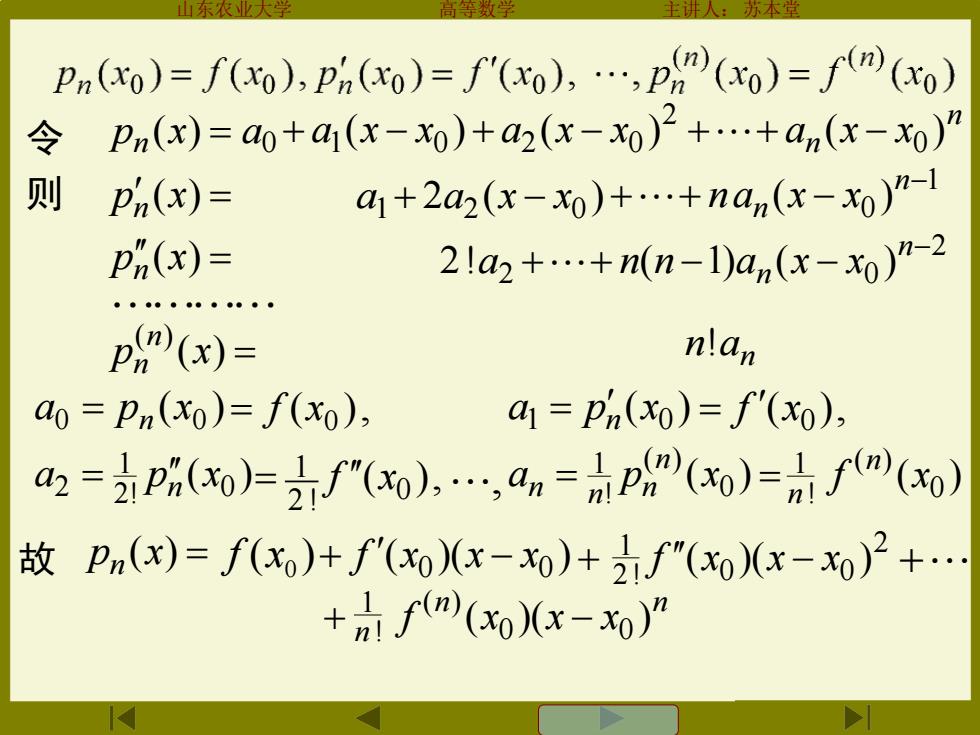
Pn(xo)=f(xo).p(xo)=f(xo).(xo)=(xo) 令 pn(x)=ao+a(x-x0)+a2(x-x0)+.+an(x-x0)" 则 p(x)= a+2a2(x-x0)++nan(x-x0)7- ph(x)= 2la2+.+n(n-1)an(x-o)n-2 p(x)= nlan ao=Pn(xo)=f(xo), 4=pn(0)=f'(xo), 4=P%(xw)=f”(x0),an=P”(xo)=fm(x) 故Pn()=f(x)+f'(ox-0)+克f"(xox-x)2+. +fm(o)(x-o)
山东农业大学 高等数学 主讲人:苏本堂 ( ) 2! 0 1 2 a p x n = ( ), 0 = f x , ( ) 0 ( ) ! 1 a p x n n = n n ( ) 0 ( ) f x n = 故 pn (x) = ( )0 f x ( )( ) 0 0 + f x x − x + 2 ! 1 ! 1 n n n f (x )(x x ) 0 0 ( ) + − ! 1 n 2 0 0 + f (x )(x − x ) 2 ! 1 令 pn (x) = 则 pn (x) = pn (x) = n an = ! ( ) ( ) p x n n ( ) 0 0 a p x = n ( ), 0 = f x ( ) 1 0 a p x n = ( ), 0 = f x a1 2 ( ) 2 0 + a x − x 1 0 ( ) − + + − n n na x x 2 2!a 2 0 ( 1) ( ) − + + − − n n n n a x x a0 n n a (x x ) a (x x ) a (x x ) 0 2 + 1 − 0 + 2 − 0 ++ −

山东农业大 3.余项估计 令R(x)=f(x)-pn(x)(称为余项),则有 R,(x)=R,(x)=.=Rm(x)=0 R,(x) (x-xo)21 Rn(x)-R.(xo)= R,(51) (51在x与x之间) (x-x0)m+1-0 (n+1)(5-x)” R,(51)-R,(xo)】 R(52) (52在x0与 (n+15-xo)”-0(n+1)n(52-xo)” 51之间 Rm(5m)-R”(x)_Rm+(5) (5在x0与X之间 (n+1).2(5m-xo)-0 (n+1)川
山东农业大学 高等数学 主讲人:苏本堂 ) 0 ( 在x 与 n 之间 ( ) ( ) 1 0 + − = n n x x R x ( 1) 2( ) ( ) 0 ( ) n x R n n n n + − = 3. 余项估计 R (x) f (x) p (x) 令 n = − n (称为余项) , ( ) 0 R x n ( ) 0 R x n = ( ) 0 0 ( ) = = R x = n n 1 0 ( ) ( ) + − n n x x R x n n n x R ( 1)( ) ( ) 1 0 1 + − = ( 1)( ) ( ) 1 0 1 n n n x R + − = 1 2 0 2 ( 1) ( ) ( ) − + − = n n n n x R = ( 1)! ( ) ( 1) + = + n R n n 则有 ( ) 0 R x − n − 0 ( ) 0 R x n − − 0 ( ) 0 ( ) R x n − n − 0 x ) 1 0 ( 在x 与x之间) 1 2 0 ( 之间 在 与 x