
第四节 反常积分 、无穷限的反常积 分 二、无界函数的反常积分
山东农业大学 高等数学 主讲人:苏本堂 第四节 反常积分 一、无穷限的反常积 分 二、无界函数的反常积分

主计 苏本堂 积分限有限 常义积分 被积函数有界 解决许多实际问题要求我们将函数x)从有限区间 推广到无限区间,将有界函数推广到无界函数.从而得到 两种反常积分(也称广义积分)】
山东农业大学 高等数学 主讲人:苏本堂 常义积分 积分限有限 被积函数有界 解决许多实际问题要求我们将函数f(x)从有限区间 推广到无限区间,将有界函数推广到无界函数.从而得到 两种反常积分(也称广义积分)
一、无穷限的反常积分 1 引例.曲线y=2 和直线x=1及x轴所围成的开口曲 边梯形的面积可记作 A- r+co dx 其含义可理解为 01 g=lim
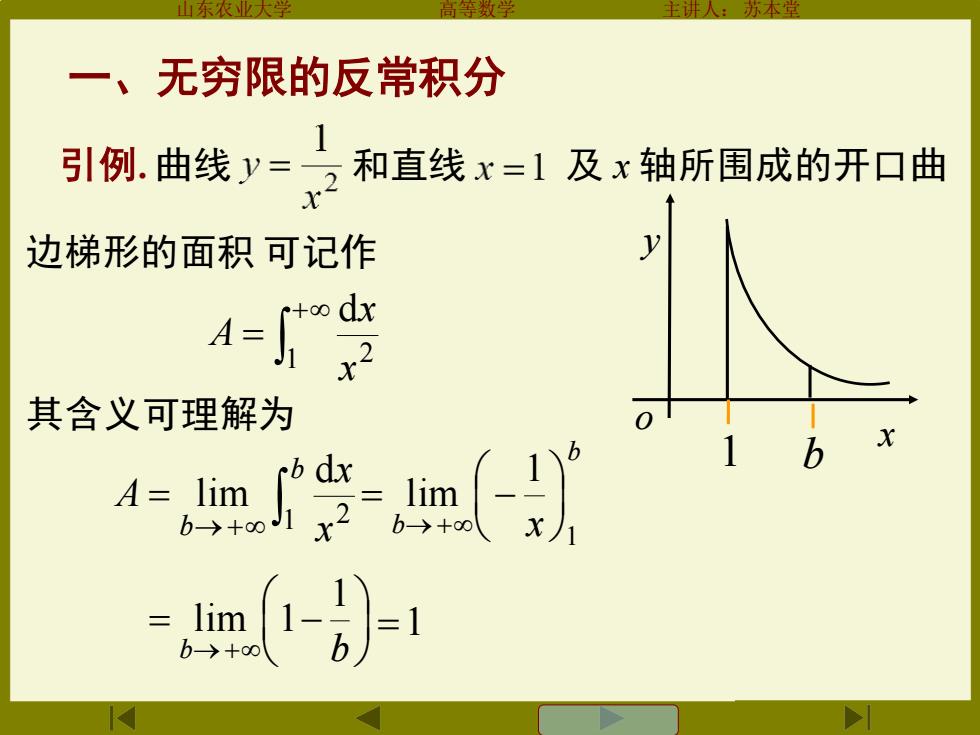
山东农业大学 高等数学 主讲人:苏本堂 一、无穷限的反常积分 引例. 曲线 和直线 及 x 轴所围成的开口曲 边梯形的面积 可记作 + = 1 2 d x x A 其含义可理解为 →+ = b b x x A 1 2 d lim b b x 1 1 lim = − →+ = − b→+ b 1 lim 1 =1 1 b y o x

方本 定义1.设f(x)∈C[a,+o),取b>a,若 nd 存在,则称此极限为f(x)的无穷限反常积分,记作 in d 这时称反常积分∫f(x)dx收敛;如果上述极限不存在, 就称反常积分∫f(x)dr发散 类似地,若f(x)∈C(-0,b],则定义 ∫fcx)dr=,limd
山东农业大学 高等数学 主讲人:苏本堂 定义1.设 f (x)C[a, + ), 取b a, 若 存在 , 则称此极限为f (x) 的无穷限反常积分, 记作 这时称反常积分 收敛 ; 如果上述极限不存在, 就称反常积分 发散 . 类似地 , 若 f (x)C(−, b], 则定义

若f(x)∈C(-0,+0),则定义 dimimd (c为任意取定的常数) 只要有一个极限不存在,就称f()d发散. 无穷限的反常积分也称为第一类反常积分 说明:上述定义中若出现0一0,并非不定型, 它表明该反常积分发散
山东农业大学 高等数学 主讲人:苏本堂 若 f (x)C(−, + ), 则定义 f x x c a a lim ( )d →− f x x b b c lim ( )d →+ + ( c 为任意取定的常数 ) 只要有一个极限不存在 , 就称 发散 . 无穷限的反常积分也称为第一类反常积分. 说明: 上述定义中若出现 − , 并非不定型 , 它表明该反常积分发散