
第七节曲率 弧微分 二、曲率及其计算公式 三、曲率圆与曲率半径
山东农业大学 高等数学 主讲人:苏本堂 第七节曲率 一、弧微分 二、曲率及其计算公式 三、曲率圆与曲率半径
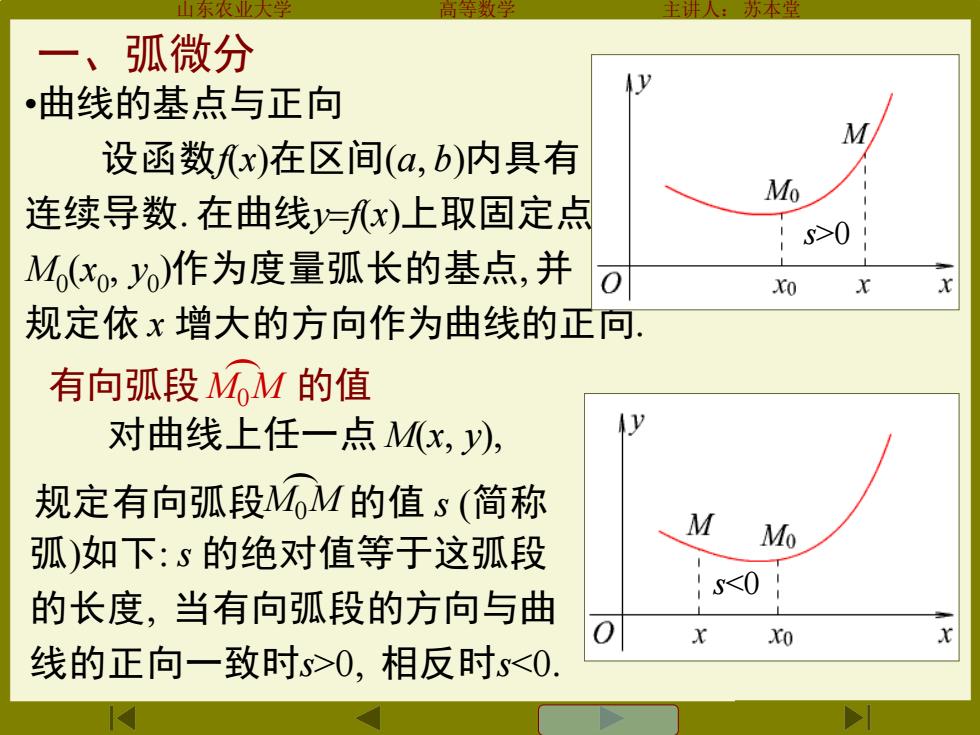
方本堂 一、弧微分 曲线的基点与正向 M 设函数x)在区间(a,b)内具有 M 连续导数.在曲线y=x)上取固定点 S>0 M,(x,)作为度量弧长的基点,并 Xo 规定依x增大的方向作为曲线的正向. 有向弧段MOM的值 对曲线上任一点Mx,y), 规定有向弧段M的值s(简称 M 弧)如下:s的绝对值等于这弧段 Mo 的长度,当有向弧段的方向与曲 S<0 Xo 线的正向一致时s>0,相反时<0:
山东农业大学 高等数学 主讲人:苏本堂 •曲线的基点与正向 设函数f(x)在区间(a b)内具有 连续导数 在曲线y=f(x)上取固定点 M0 (x0 y0 )作为度量弧长的基点 并 规定依 x 增大的方向作为曲线的正向 一、弧微分 有向弧段M0M 的值 ( 弧)如下 s 的绝对值等于这弧段 的长度 当有向弧段的方向与曲 线的正向一致时s>0 相反时s<0 s<0 对曲线上任一点 M(x y) M0M ( 规定有向弧段 的值 s (简称 s>0
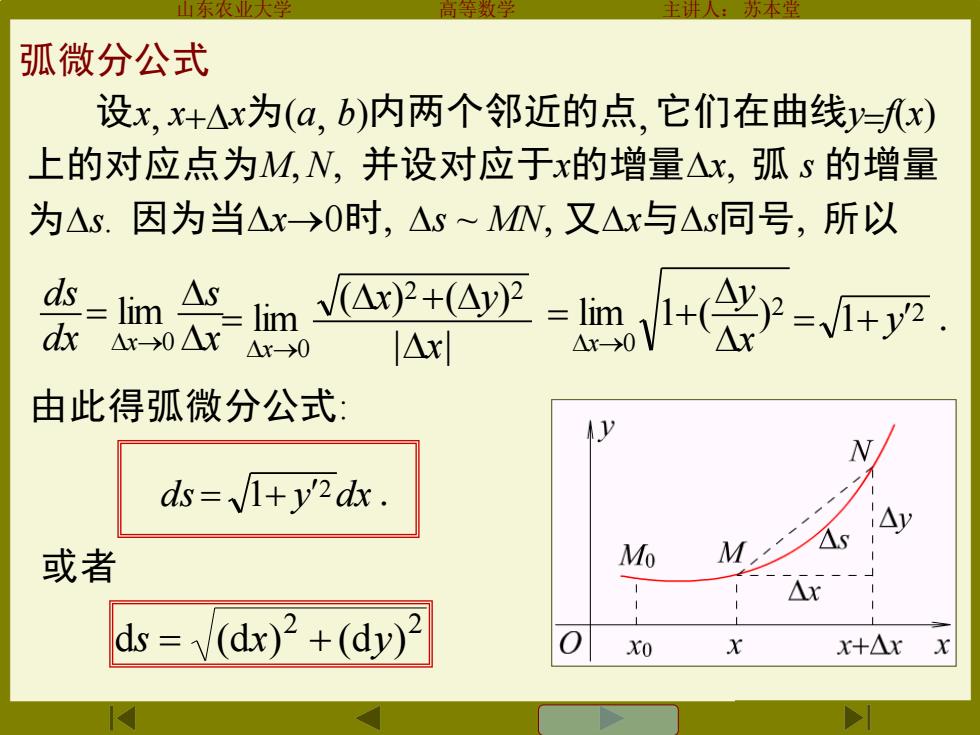
弧微分公式 设x,+△x为(a,b)内两个邻近的点,它们在曲线=孔x) 上的对应点为M,W,并设对应于x的增量△x,弧s的增量 为△s.因为当△x→0时,△s~MN,又△x与As同号,所以 4 =lim dx -lim △x0△X x-0 I△x| 由此得弧微分公式: ds=+y'2dx. 或者 Mo M △S △x ds =/(dx)2+(dy)2 XO x+△x
山东农业大学 高等数学 主讲人:苏本堂 上的对应点为M N 并设对应于x的增量Dx 弧 s 的增量 为Ds. 因为当Dx→0时 Ds ~ MN 又Dx与Ds同号 所以 由此得弧微分公式: 2 0 2 2 0 0 lim 1 ( ) | | ( ) ( ) lim lim x y x x y x s dx ds x x x D D = + D D + D = D D = D → D → D → 1 2 = + y ds y dx 1 2 = + 2 0 2 2 0 0 lim 1 ( ) | | ( ) ( ) lim lim x y x x y x s dx ds x x x D D = + D D + D = D D = D → D → D → 2 0 2 2 0 0 lim 1 ( ) | | ( ) ( ) lim lim x y x x y x s dx ds x x x D D = + D D + D = D D = D → D → D → 或者 2 2 ds = (dx) + (dy) 弧微分公式 设x x+Dx为(a b)内两个邻近的点 它们在曲线y=f(x)
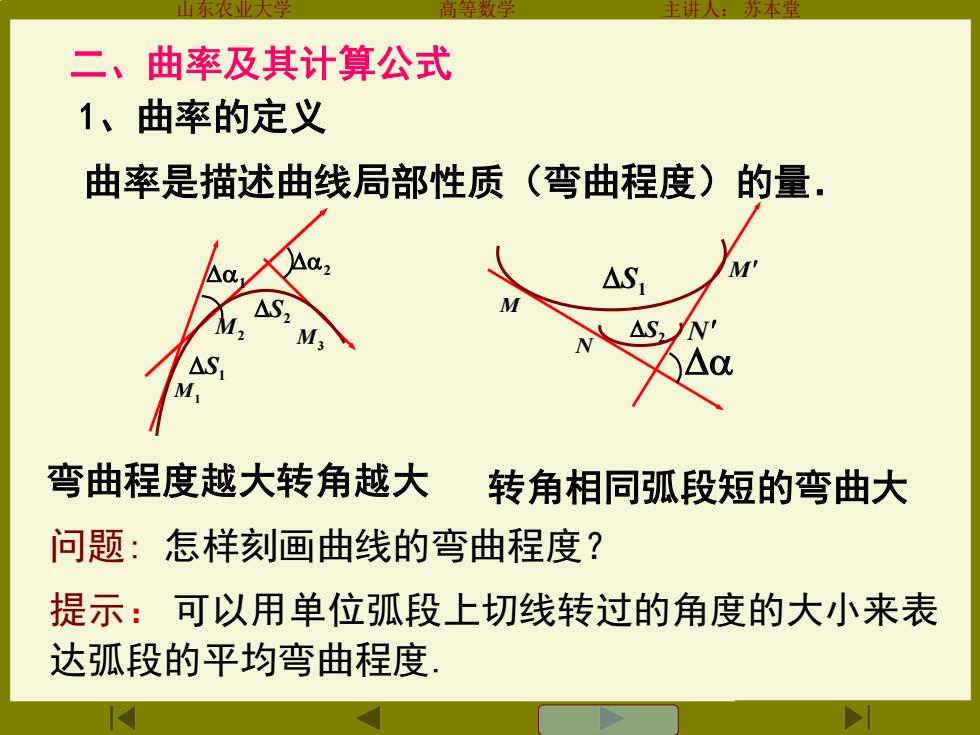
山东农业大 主进 方本堂 二、曲率及其计算公式 1、曲率的定义 曲率是描述曲线局部性质(弯曲程度) 的量 M 弯曲程度越大转角越大: 转角相同弧段短的弯曲大 问题:怎样刻画曲线的弯曲程度? 提示:可以用单位弧段上切线转过的角度的大小来表 达弧段的平均弯曲程度
山东农业大学 高等数学 主讲人:苏本堂 曲率是描述曲线局部性质(弯曲程度)的量. M M DS1 DS2 N N D 弯曲程度越大转角越大 转角相同弧段短的弯曲大 1、曲率的定义 M1 M3 D2 M2 DS2 DS1 D1 二、曲率及其计算公式 问题: 怎样刻画曲线的弯曲程度? 提示: 可以用单位弧段上切线转过的角度的大小来表 达弧段的平均弯曲程度
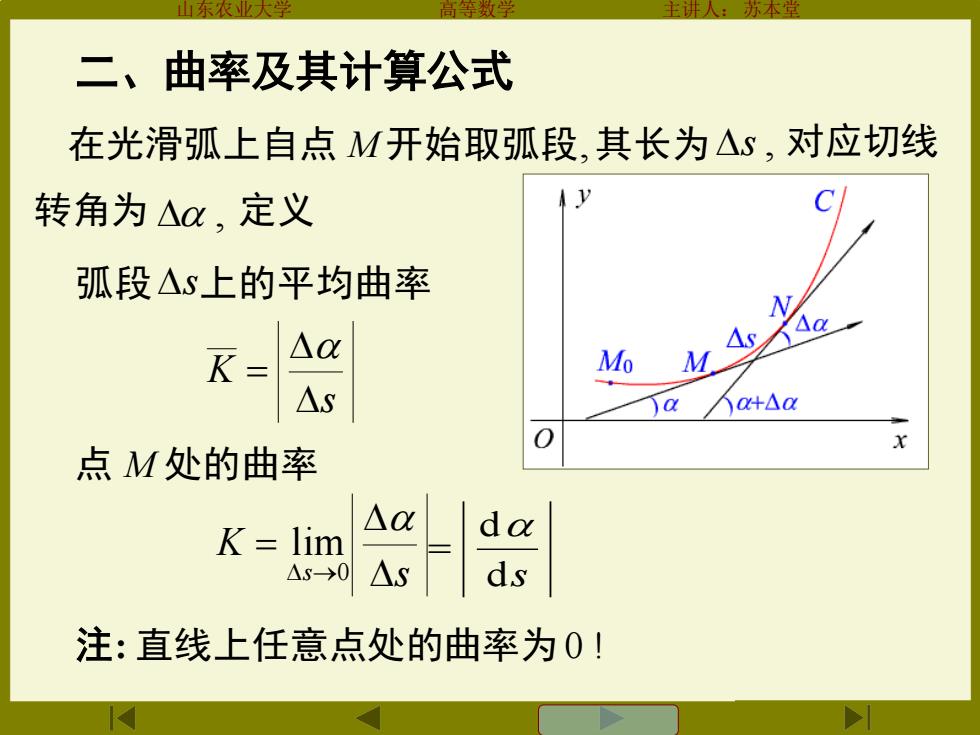
二、曲率及其计算公式 在光滑弧上自点M开始取弧段,其长为△s,对应切线 转角为△,定义 弧段△s上的平均曲率 K- △ Mo M △s a a+△a 点M处的曲率 K=lim △0 △5→0 △S ds 注:直线上任意点处的曲率为0!
山东农业大学 高等数学 主讲人:苏本堂 二、曲率及其计算公式 在光滑弧上自点 M 开始取弧段, 其长为 Ds , 对应切线 D , 定义 弧段 Ds 上的平均曲率 s K D D = 点 M 处的曲率 s K s D D = D → 0 lim ds d = 注: 直线上任意点处的曲率为 0 ! 转角为