
苏本宜 1.曲边梯形的面积 元素法 f() =f(x) 1化整为零 2以直代曲 (以常代变) △S:≈f(5:)△x: 3积零为整 防a S≈ 分法越细,越接近精确值 a x X2 5 Xn-1 b
山东农业大学 高等数学 主讲人:苏本堂 xi xi+1 1 x i x2 元素法 1 化整为零 2 以直代曲 (以常代变) i i xi S f ( ) 3 积零为整 y x o y=f (x) n−1 x = n i i xi S f 1 ( ) a b . . 分法越细,越接近精确值 1. 曲边梯形的面积 f (i )

山东农业大 导效 主 苏本堂 1.曲边梯形的面积 元素法 yf(x) 1化整为零 2以直代曲 (以常代变) △S,≈f(5)△c: 3积零为整 S≈ ∑f5)△x, i= 分法越细,越接近精确值 4取极限 5 令分法无限变细 i+1 b
山东农业大学 高等数学 主讲人:苏本堂 xi i xi+1 元素法 4 取极限 y x o y=f (x) 令分法无限变细 . a . b . . 分法越细,越接近精确值 1 化整为零 2 以直代曲 (以常代变) 3 积零为整 = n i i xi S f 1 ( ) i i xi S f ( ) f (i ) 1. 曲边梯形的面积
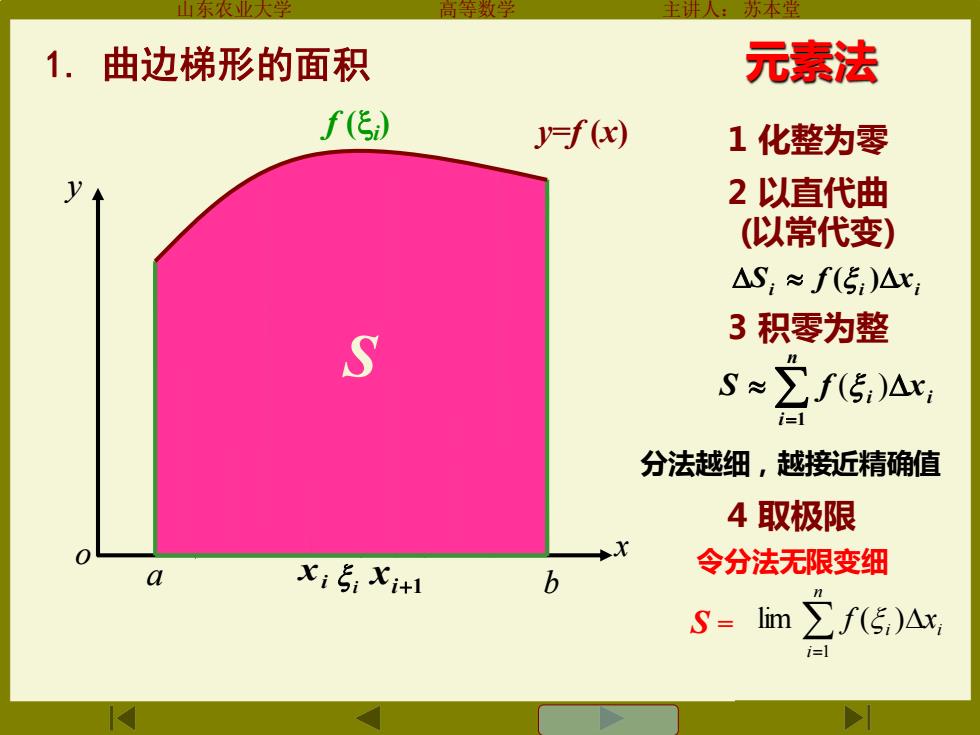
1.曲边梯形的面积 元素法 f(传) =f(x) 1化整为零 2以直代曲 (以常代变) △S:≈f(5:)△x 3积零为整 )ar S≈ 分法越细,越接近精确值 4取极限 Xi+ 令分法无限变细 b S=m∑f(5,)Ax, i=1
山东农业大学 高等数学 主讲人:苏本堂 xi i xi+1 元素法 4 取极限 y x o y=f (x) 令分法无限变细 . . . . 分法越细,越接近精确值 1 化整为零 2 以直代曲 (以常代变) 3 积零为整 = n i i xi S f 1 ( ) i i xi S f ( ) f (i ) = n i i i f x 1 S = lim ( ) . S . a b 1. 曲边梯形的面积