
主 第二节 微积分基本公式 一、引例 二、积分上限的函数及其导数 三、牛顿一莱布尼茨公式
山东农业大学 高等数学 主讲人:苏本堂 第二节 微积分基本公式 三、牛顿—莱布尼茨公式 一、引例 二、积分上限的函数及其导数

引例 设物体从某定点开始作直线运动,在时刻物体所经 过的路程为S(),速度为v=v(t)=S(t)(v(t)≥0),则在时间间隔 [T,T,]内物体所经过的路程S可表示为 ST)-ST)及0d, 即 d=S)-SG). 上式表明,速度函数v()在区间[T,T]上的定积分等 于()的原函数S(t)在区间[T,T]上的增量 这个特殊问题中得出的关系是否具有普遍意义呢?
山东农业大学 高等数学 主讲人:苏本堂 设物体从某定点开始作直线运动, 在t时刻物体所经 过的路程为S(t), 速度为v=v(t)=S(t)(v(t)0), 则在时间间隔 [T1 , T2 ]内物体所经过的路程S可表示为 上式表明, 速度函数v(t)在区间[T1 , T2 ]上的定积分等 于v(t)的原函数S(t)在区间[T1 , T2 ]上的增量. 这个特殊问题中得出的关系是否具有普遍意义呢? ( ) ( ) S T2 −S T1 及 v t dt T T ( ) 2 1 即 ( ) ( ) ( ) 2 1 2 1 v t dt S T S T T T = − 即 一、引例
等数 二、积分上限的函数及其导数 定理1.若f(x)∈C[a,b],则变上限函数 Φ(x)=∫f)dt 是f(x)在[a,b]上的一个原函数 Φ() 证:x,x+h∈[a,b],则有 xx+hb x x+w-f0d-0] h 打f@a=f5(<E<x+分 .'f(x)∈C[a,b] ∴.Φ'(x)=lim Φ(x+h)-Φ(x) 2 =limf()=f(x) h-→0 h h-→0
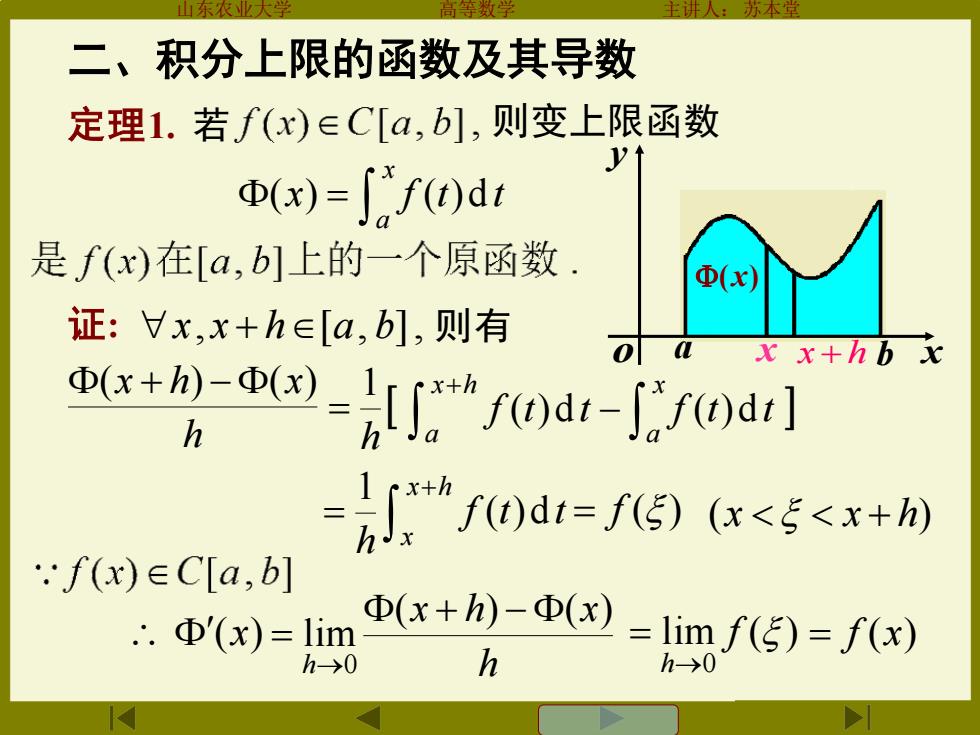
山东农业大学 高等数学 主讲人:苏本堂 二、积分上限的函数及其导数 则变上限函数 = x a (x) f (t)dt 证: x, x + h[a, b], 则有 h (x + h) −(x) h 1 = − + x a x h a f (t)dt f (t)dt + = x h x f t t h ( )d 1 = f () (x x + h) h x h x h ( ) ( ) lim 0 + − = → lim ( ) 0 f h→ (x) = = f (x) 定理1. 若 a b x y o x + h (x) x

注: 1)定理1证明了连续函数的原函数是存在的.同时为 通过原函数计算定积分开辟了道路. 2)变限积分求导&」/0)dr-fa侧 品foar-imwp四 dlod-+。ona =f[p(x)]p'(x)-f[w(x)]W(x)
山东农业大学 高等数学 主讲人:苏本堂 注: 1) 定理 1 证明了连续函数的原函数是存在的. 2) 变限积分求导: ( ) ( )d d d x a f t t x = f [(x)](x) 同时为 通过原函数计算定积分开辟了道路 . ( ) ( ) ( )d d d x x f t t x = f [(x)](x) − f [(x)](x) + = ( ) ( ) ( )d ( )d d d x a a x f t t f t t x

主计 方本 例1.求lim x→0 x2 2 解:原式 -limeco.(←sin) x→0 2x 2e 例2.确定常数a,b,c的值,使 ax-sinx lim =c(c≠0) d+2)d 解::x→0时,ax-sinx→0,c≠0,.b=0. 原式=lim a-cosx a-cosx lim =C x0ln(1+x2) c0,故a=1.又由1-c0sxx2,得c=2:
山东农业大学 高等数学 主讲人:苏本堂 ( sin ) 2 cos e x x − − 例1. 求 解: 原式 0 lim → = − x 2x 2e 1 = 例2. 确定常数 a , b , c 的值, 使 解: b = 0. 原式 = c ≠0 , 故 a =1. 又由 ~ , 得 . 2 1 c =