
主进 苏本堂 第六节函数的图像的描绘 一、曲线的渐近线 二、函数图像的描绘
山东农业大学 高等数学 主讲人:苏本堂 第六节函数的图像的描绘 二、函数图像的描绘 一、 曲线的渐近线

一、曲线的渐近线 定义.若曲线C上的点M沿着曲线无限地远离原点 时,点M与某一直线L的距离趋于0,则称直线L为 曲线C的渐近线. y=f(x) 或为“纵坐标差” y=kx+b 例如,双曲线 a 有渐近线 x±=0 a b 但抛物线y=x2无渐近线
山东农业大学 高等数学 主讲人:苏本堂 一、 曲线的渐近线 无渐近线 . 点 M 与某一直线 L 的距离趋于 0, 定义 . 若曲线 C上的点M 沿着曲线无限地远离原点 时, 则称直线 L 为 曲线C 的渐近线 . 例如, 双曲线 有渐近线 = 0 b y a x 但抛物线 或为“纵坐标差” N L y = k x +b M x y o C y = f (x) P x y o

山东农业大 1.水平与铅直渐近线 若limf(x)=b,则曲线y=f(x)有水平渐近线y=b. (或x→-∞) 若1imf(x)=oo,则曲线y=f(x)有垂直渐近线x=xo. x→x0 (或x→x) 例1.求曲线y= +2的渐近线 x-1 解:lim( +2)=2 x→0X-1 .y=2为水平渐近线; 1 :lim(,+2)=o,∴.x=1为垂直渐近线 x→1x-1
山东农业大学 高等数学 主讲人:苏本堂 1. 水平与铅直渐近线 若 则曲线 有水平渐近线 y = b. (或x → −) 若 则曲线 有垂直渐近线 . 0 x = x ( ) 0 → − 或x x 例1. 求曲线 的渐近线 . 解: 2) 2 1 1 lim ( + = x→ x − y = 2 为水平渐近线; 2) , 1 1 lim( 1 + = x→ x − x =1 为垂直渐近线. 2 1

2.斜渐近线 (P76题14) 若1im[f(x)-(x+b)]=0,则曲线y=f(x)有 X→+00 (或x→-o0) 斜渐近线y=kx+b lim [f(x)-(kx+b)]=0 X→十00 k=lim /(x) b X→+00 X X 2-k b1=0 lim f(x) x-→+00X (或x→-0) lim 01=0 b=lim[f(x)-kx灯] x→十00 L (或x→-o)
山东农业大学 高等数学 主讲人:苏本堂 2. 斜渐近线 斜渐近线 y = kx + b. (或x → −) 若 (kx + b) ] 0 ( ) lim [ − − = →+ x b k x f x x x (kx + b) ] 0 ( ) lim [ − − = →+ x b k x f x x ] ( ) lim [ x b x f x k x = − →+ x f x k x ( ) lim →+ = b lim [ f (x) kx] x = − →+ (或x → −) (或x → −) ( P76 题14)
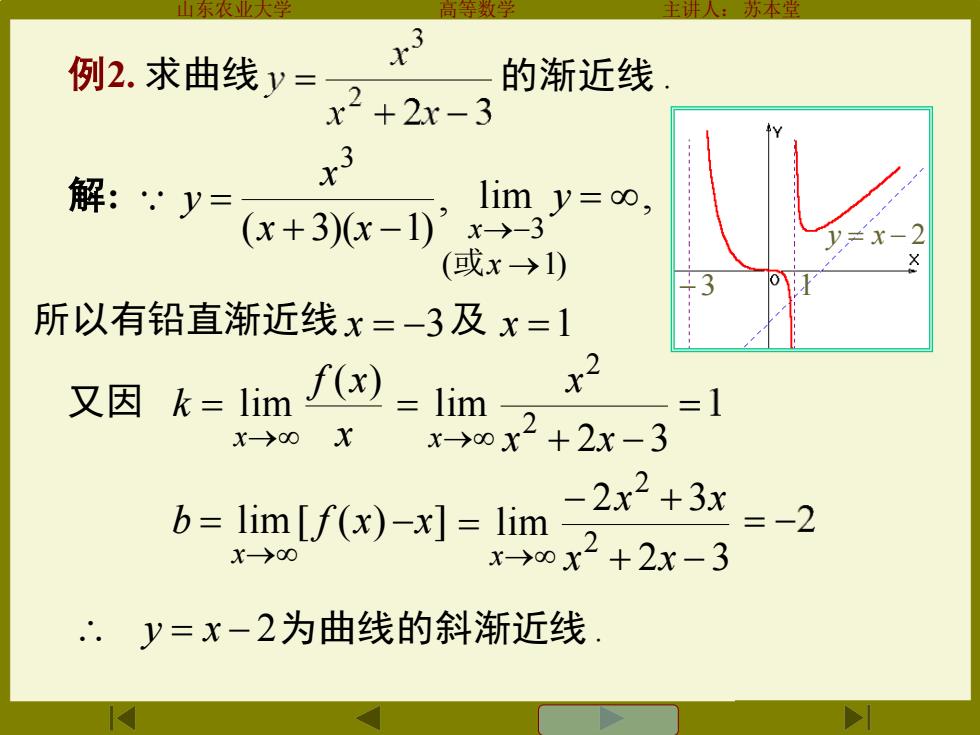
本堂 例2.求曲线y= 2+2x-3 的渐近线 解:y x3 lim y=co, (x+3)x-1)x-→-3 (或x→1) +3 所以有铅直渐近线x=-3及x=1 又因k=limf) =1im x =1 X-→00X x-→0x2+2x-3 -2x2+3x b=lim [f(x)-x]=lim- 三一2 X>00 x0x2+2x-3 y=x-2为曲线的斜渐近线
山东农业大学 高等数学 主讲人:苏本堂 例2. 求曲线 的渐近线 . 解: , ( 3)( 1) 3 + − = x x x y lim , 3 = →− y x (或x →1) 所以有铅直渐近线 x = −3 及 x =1 又因 x f x k x ( ) lim → = 2 3 lim 2 2 + − = → x x x x b lim[ f (x) x] x = − → 2 3 2 3 lim 2 2 + − − + = → x x x x x y = x − 2为曲线的斜渐近线 . −3 1 y = x − 2