
大 人术 第二节定积分在几何学上的应用 平面图形的面积 二 体积 三 平面曲线的弧长
山东农业大学 高等数学 主讲人:苏本堂 第二节 定积分在几何学上的应用 一 平面图形的面积 二 体积 三 平面曲线的弧长

山东农业大 方本 一、平面图形的面积 1、直角坐标系情形 ↑y=f(x) A="f(x)d o a r+△b y=f2(x) x=81y) y+dy x=82y) fi(x) o a 七x+b o A=[Lf(x)-f(x)ld A=[g2(y)-g(y)ldx
山东农业大学 高等数学 主讲人:苏本堂 一、平面图形的面积 x y o y = f (x) a b = b a A f (x)dx = − b a A [ f2 (x) f1 (x)]dx xx + x 1 、直角坐标系情形 x y o ( ) y = f 1 x ( ) y = f 2 x a x x + dx b x y o c d ( ) 1 x = g y ( ) 2 x = g y y y + dy = − b a A [g (y) g (y)]dx 2 1
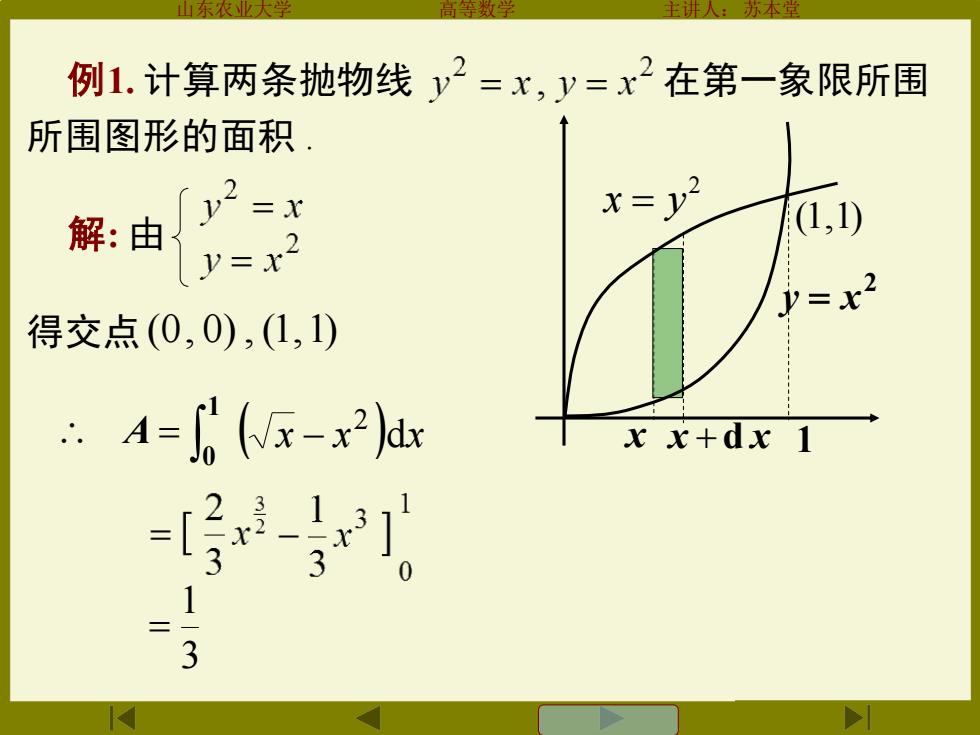
例1.计算两条抛物线y2=x,y=x2在第一象限所围 所围图形的面积 解:由 y-=x (1,1) 2 y=x 得交点(0,0),(1,1) P=x2 ·A=(x-x2d xx+dx 1 3
山东农业大学 高等数学 主讲人:苏本堂 例1. 计算两条抛物线 在第一象限所围 所围图形的面积 . 2 y = x x x + d x 解: 由 得交点 (0, 0) , (1,1) (1,1) d A ( x x )dx 1 2 = − 3 1 = = 1 0 A 2 x = y
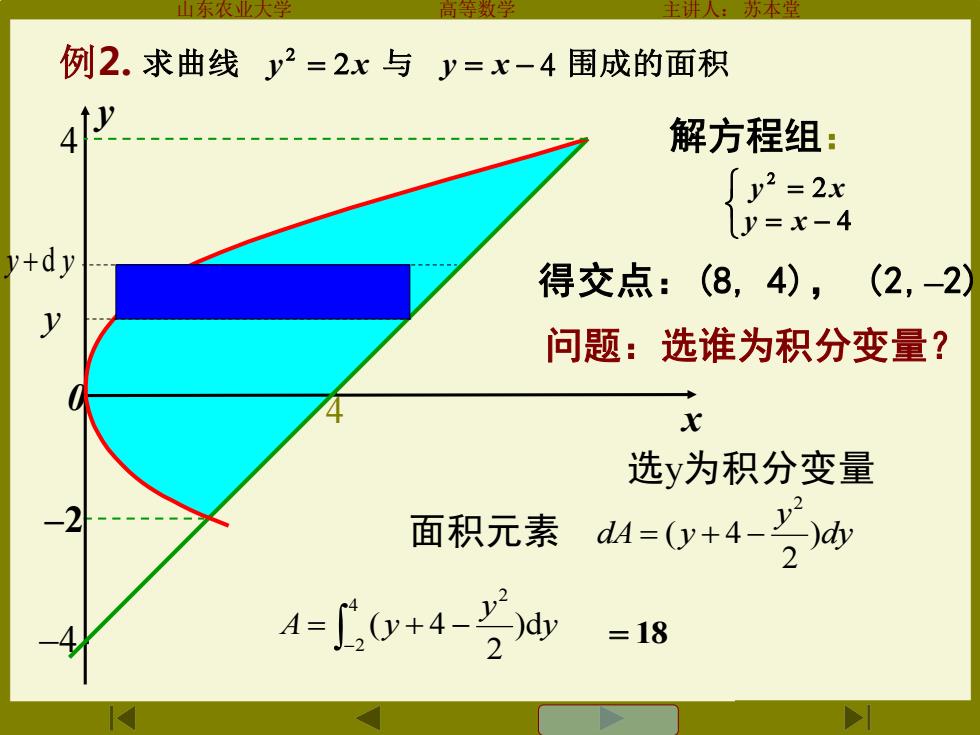
山东农少大 主讲 本堂 例2.求曲线y2=2x与y=x-4围成的面积 解方程组: {y2=2x y=x-4 v+dy 得交点:(8,4),(2,-2) y 问题:选谁为积分变量? x 选y为积分变量 面积元素 d1=0y+4-y A=0+4 =18
山东农业大学 高等数学 主讲人:苏本堂 求曲线 = 与 = − 4 围成的面积 y x y x –2 。 。 0 y x 例2. 4 4 –4 解方程组: = − = y x y x 得交点:(8, 4), (2,–2) 问题:选谁为积分变量? )d 2 ( 4 2 4 2 y y A = y + − − = 18 选y为积分变量 面积元素 ) 2 ( 4 2 dy y dA = y + − y y + d y

2 例3.求椭圆 2+ =1所围图形的面积. 解:利用对称性,有dA=ydx 4=4dx 利用椭圆的参数方程 x=acost l y=bsint (0≤t≤2π) 应用定积分换元法得 A=4 bsint.(-asint)dt inrd =4ab:2受=xab 当a=b时得圆面积公式
山东农业大学 高等数学 主讲人:苏本堂 a b o x y x 例3. 求椭圆 解: 利用对称性 , d A = y dx 所围图形的面积 . 有 = a A y x 0 4 d 利用椭圆的参数方程 (0 2 ) sin cos = = t y b t x a t 应用定积分换元法得 = 2 0 2 4 sin d ab t t = 4ab 2 1 2 = ab 当 a = b 时得圆面积公式 x + d x