第三节频率与概率 讨论如何表征随机事件在一次试验中 发生的可能性的大小 频率 概率
第三节 频率与概率 ——讨论如何表征随机事件在一次试验中 发生的可能性的大小 频率 概率

一、频率 定义、在相同的条件下,进行了n次试验,在这n次试 验中,事件A发生的次数n,称为事件A发生的频数。比值 ”,n称为事件4发生的频率,并记成4.即④=元 基本性质: (⑩0≤f(A)≤1; (2)f(S)=1,f(②)=0; (3) 若A,A2,A是两两互不相容的事件,则 f(AUA2U.UA)=f(A)+f (A2)++(A) 说明:频率反映了在n次试验中,事件A发生的频繁程度; 频率越大,事件A在一次试验中发生的可能性就越大
定义 在相同的条件下,进行了 n 次试验,在这 n 次试 验中,事件 A 发生的次数nA 称为事件 A 发生的频数。比值 / n n A 称为事件 A 发生的频率,并记成 ( ) n f A 。 一、频率 (1) 0 ( ) 1; n f A (2) ( ) 1, ( ) 0; f S f = = (3) 若 1 2 , , , A A Ak是两两互不相容的事件,则 1 2 1 2 ( ) ( ) ( ) ( ) k n n n k f A A A f A f A f A = + + + 基本性质: 即 ( ) A n n f A n = 说明:频率反映了在n 次试验中,事件A发生的频繁程度; 频率越大,事件A在一次试验中发生的可能性就越大
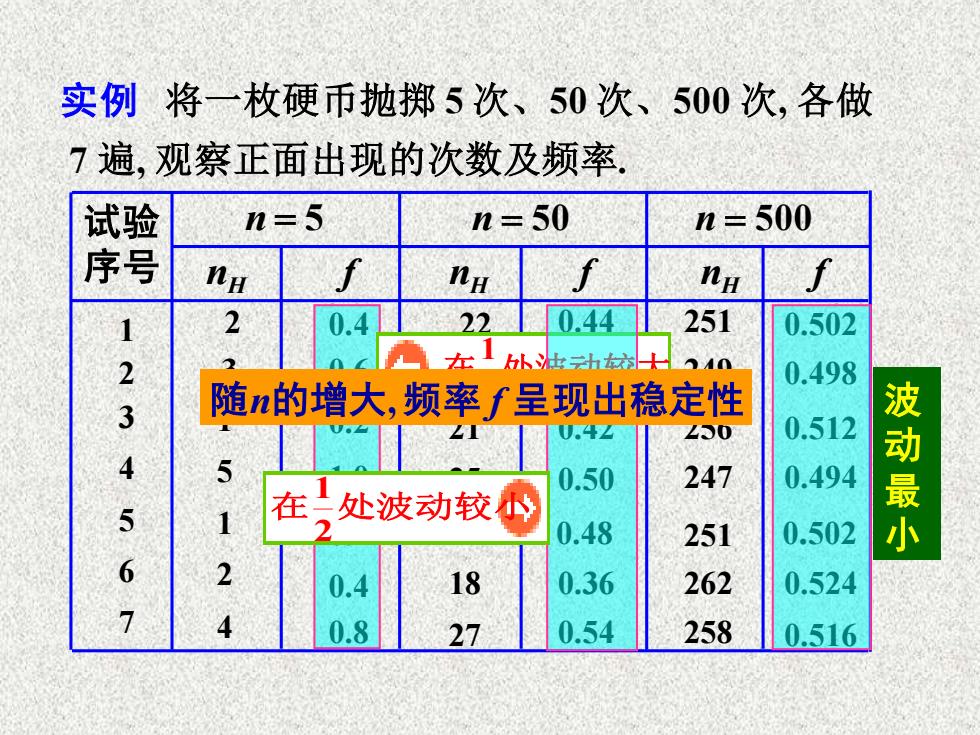
实例将一枚硬币抛掷5次、50次、500次,各做 7遍,观察正面出现的次数及频率 试验 n=5 n=50 n=500 序号 na ng f ng f 1 2 0.4 22 0.44 251 0.502 产在1从h给士 0.498 3 随n的增大,频率f呈现出稳定性 U.4☑ Z50 0.512 4 5 0.50 247 0.494 5 1 在二处波动较心 0.502 波动最小 0.48 251 6 2 0.4 18 0.36 262 0.524 7 0.8 27 0.54 258 0.516
实例 将一枚硬币抛掷 5 次、50 次、500 次, 各做 7 遍, 观察正面出现的次数及频率. 试验 序号 n = 5 nH f 1 2 3 4 5 6 7 2 3 1 5 1 2 4 nH f n = 50 22 25 21 25 24 18 27 nH n = 500 251 249 256 247 251 262 258 0.4 0.6 0.2 1.0 0.2 0.4 0.8 0.44 0.50 0.42 0.48 0.36 0.54 f 0.502 0.498 0.512 0.494 0.524 0.516 0.50 0.502 在 处波动较大 2 1 在 处波动较小 2 1 波 动 最 小 随n的增大, 频率 f 呈现出稳定性
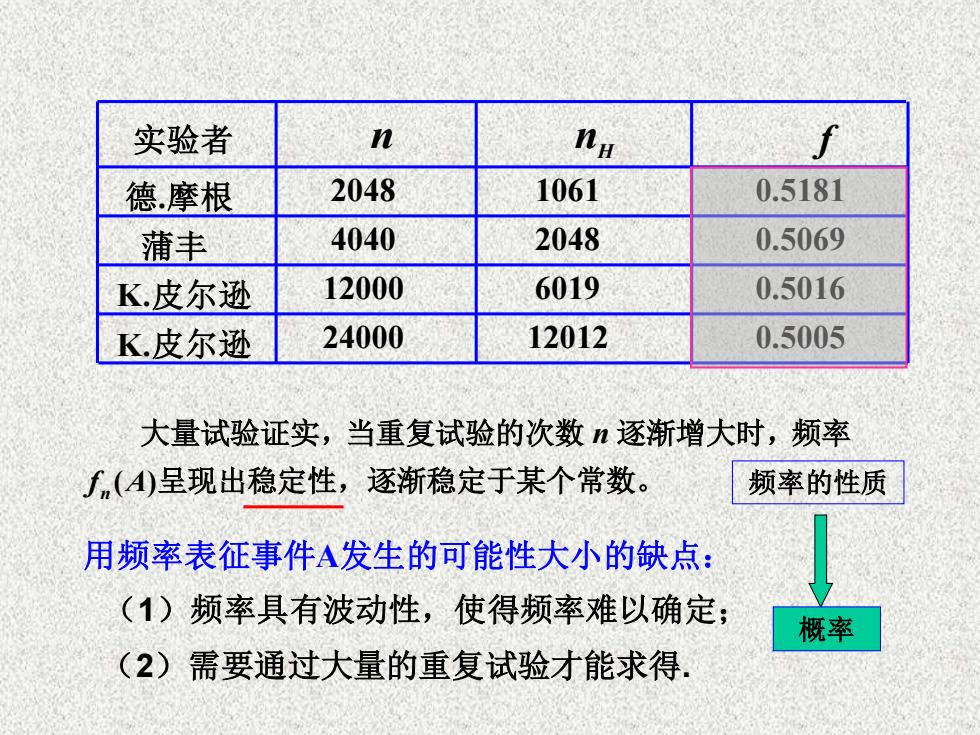
实验者 n Hu f 德摩根 2048 1061 0.5181 蒲丰 4040 2048 0.5069 K皮尔逊 12000 6019 0.5016 K皮尔逊 24000 12012 0.5005 大量试验证实,当重复试验的次数n逐渐增大时,频率 f(A)呈现出稳定性,逐渐稳定于某个常数。 频率的性质 用频率表征事件A发生的可能性大小的缺点: (1)频率具有波动性,使得频率难以确定; 概率 (2)需要通过大量的重复试验才能求得:
实验者 德.摩根 蒲丰 K.皮尔逊 K.皮尔逊 n nH f 2048 1061 0.5181 4040 2048 0.5069 12000 6019 0.5016 24000 12012 0.5005 大量试验证实,当重复试验的次数 n 逐渐增大时,频率 ( ) n f A 呈现出稳定性,逐渐稳定于某个常数。 用频率表征事件A发生的可能性大小的缺点: (1)频率具有波动性,使得频率难以确定; 频率的性质 概率 (2)需要通过大量的重复试验才能求得

二、概率 1933年,苏联数学家柯尔莫哥洛夫提出了概率论的公理化 结构,给出了概率的严格定义,使概率论有了迅速的发展。 Andrey Nikolaevich Kolmogorov (1903-1987)
二、概率 1933 年,苏联数学家柯尔莫哥洛夫提出了概率论的公理化 结构,给出了概率的严格定义,使概率论有了迅速的发展。 (1903 – 1987) Andrey Nikolaevich Kolmogorov