f(x) (二)指数分布 3 设连续型随机变量X的概率密度为 21/3 心 0=1 0=2 3 其中0>0为常数,则称X服从参数为的指数分布,记作X~e(0) 易知()fx)≥0,(2小fx)k=1 F(x 0.9 其分布函数为 0-2 r- x>0 0.4 x≤0 0.3 0.2 0.1 2345678910
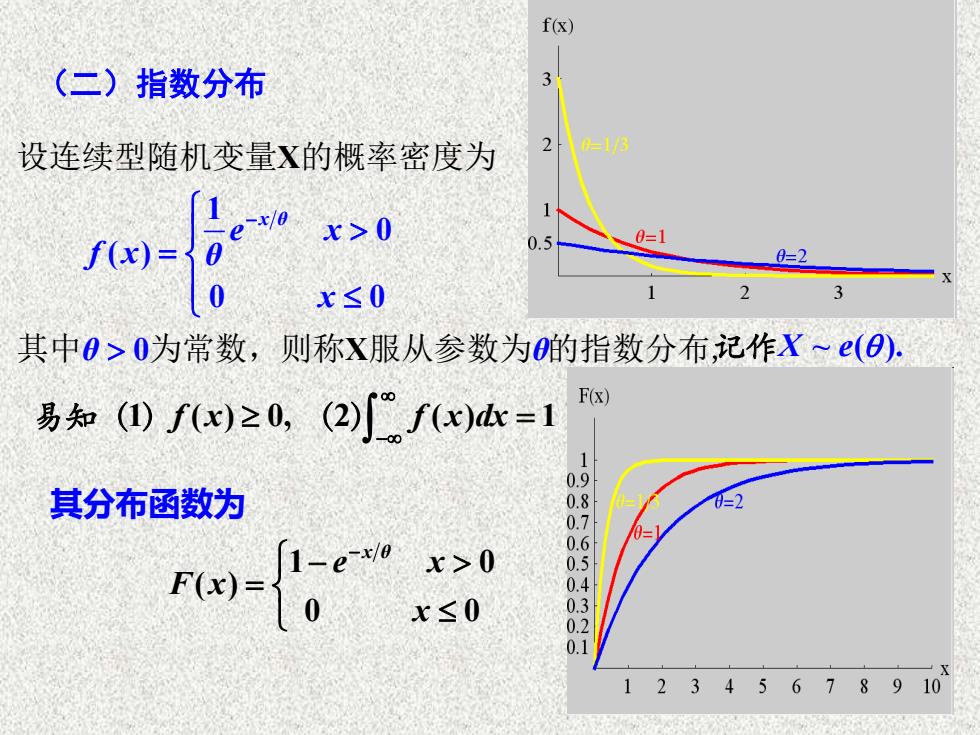
(二)指数分布 其分布函数为 1 0 ( ) 0 0 0 X X 设连续型随机变量 的概率密度为 其中 为常数,则称 服从参数为 的指数分布, x θ e x f x θ x θ θ − = 1 ( ) 0, 2 ( ) 1 f x f x dx − = 易知( ) ( ) 1 0 ( ) 0 0 x θ e x F x x − − = 记作X e ~ ( ).

指数分布的特性:无记忆性 F() 1-e-x/o x>0 0 x≤0 设X服从参数为0的指数分布,对于任意,>,有 PiX>s+tx>s=PiX>t. 证明:P{X>S+t|X>s} P{X>s+0∩(X>}_PX>s+ P(X>s P(X>s 1-F(s+) 1-F(S) erteauo =PXt. 补例.设某灯管寿命X~(2000)(单位:小时) (1)任取一灯管,求能正常使用500小时以上的概率 (2)有一只灯管已经正常使用了1000小时以上,求还能使用500 小时以上的概率
P X s t X s { | } + ( ) ( ) { } P X s t X s P X s + = { } { } P X s t P X s + = 1 ( ) 1 ( ) F s t F s − + = − ( )/ / s t s e e − + − = t/ e − = = P X t { }. 指数分布的特性: 设X s t 服从参数为的指数分布,对于任意 , 0 ,有 无记忆性 1 0 ( ) 0 0 x θ e x F x x − − = = P X t { }. 补例. 设某灯管寿命X ~ e(2000)(单位:小时) (1)任取一灯管, 求能正常使用500小时以上的概率. (2) 有一只灯管已经正常使用了1000 小时以上,求还能使用500 小时以上的概率. 证明:P X s t X s { | } +