
一、连续型随机变量及其概率密度的概念与性质 1.定义 如果对于随机变量X的分布函数F(x),存在非负函数f(x), 使对于任意实数x有Fx)=」nfu)d, 则称X为连续型随机变量,其中f(x)称为X的概率密度函数, 简称概率密度。 例如: 0,x<0, F(x)={ 40≤x<2,f0= 0<t<2, 1,x≥2. 0,其它. 说明:连续型随机变量X的分布函数F(x)是连续函数
一、连续型随机变量及其概率密度的概念与性质 1. 定义 ( ) ( ) ( ( )d , ) x X f x F x f F x x t t − = 如果对于随机变量 的分布函数 ,存在 , 使对于任意实数 有 非负函数 , ( ) . 则称 X f 为连续型随机变量 其中 x 称为 X的概率密度 , 简称概 数 率密度 函 例如: 2 0, 0, ( ) , 0 2, 4 1, 2. x x F x x x = , 0 2, ( ) 2 0, . 其它 t t f t = 说明:连续型随机变量X的分布函数F x( ) . 是连续函数
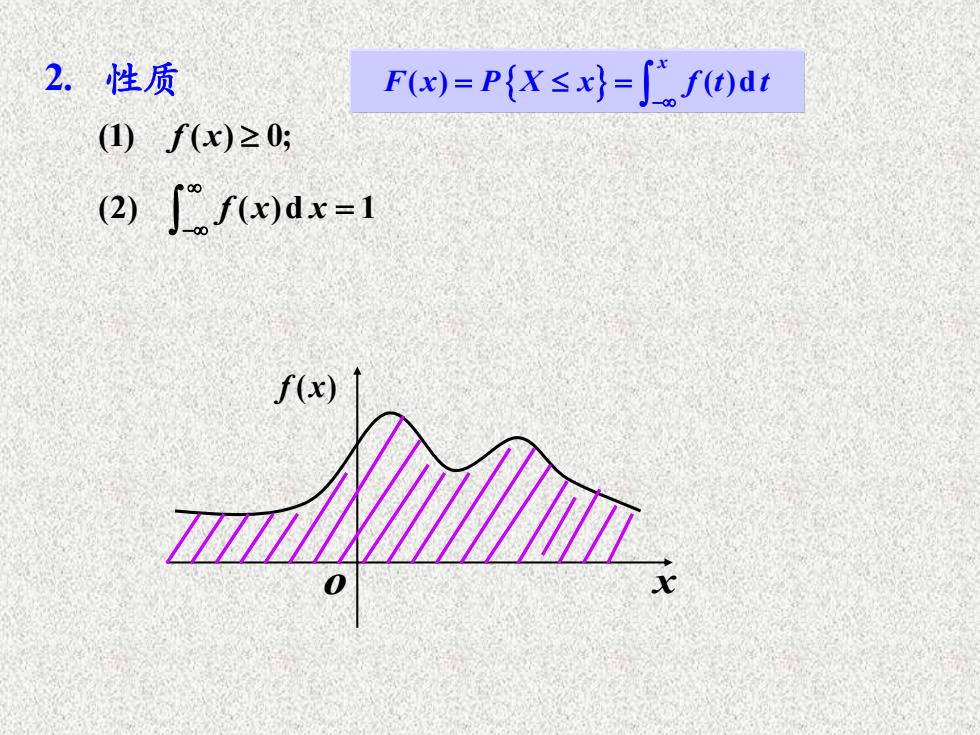
2.性质 Fx)=P{X≤x}=∫f)dt (I)f(x)≥0; 2)∫fx)dx=1 f(x)
(1) ( ) 0; f x (2) ( )d 1 f x x − = 2. 性质 ( ) ( )d x F x P X x f t t − = = o x f x( )

2.性质 Fx)=P{X≤x}=∫f)d (1)f(x)≥0; (2)∫fx)dx=1 (3) 对于任意实数x1,x2(x1≤x2) Px<X≤x}=Fc,)-Fx)=Jfx)dx. 证明: 同时得以下计算公式 PX≤a=F(a=∫nfx)dx, PX>m=1-PX≤m=1-Fo)=∫f(x)dx (4)若f(x)在,点x处连续,则有F(x)=f(x) 说明:1)P{x,<X≤x2}为相应曲边梯形的面积
(1) ( ) 0; f x (2) ( )d 1 f x x − = 1 2 1 2 (3) , ( ) 对于任意实数 x x x x 2. 性质 1 2 P x X x { } 2 1 2 1 ( ) ( ) ( )d . x x = − = F x F x f x x ( ) ( )d x F x P X x f t t − = = 证明: P X a F a { } ( ) = ( )d , a f x x − = P X a P X a { } 1 { } = − = −1 ( ) F a ( )d . a f x x = 同时得以下计算公式 (4) ( ) , 若 f x x 在点 处连续 则有 F x f x ( ) ( ). = 说明: 1 { } )P x X x 1 2 为相应曲边梯形的面积

说明: 2)P{x<X<x+△x≈f(x)△x(△x很小) 3)若X为连续型随机变量,则对任一实数, 有P{X=d=0. >P{a≤X≤b}=P{a<X≤b}=P{a≤X<b} =Pa<X<b}=∫fx)dx 概率为0的事件不一定是不可能事件。 同样,概率为1的事件也不一定是必然事件。 若为离散型随机变量, {X=}是不可能事件台P{X==0
2)P x X x x f x x x { } ( + ) ( 很小) 3)若X 为连续型随机变量,则对任一实数 a, 有 P{X=a}=0. P a X b { } = P a X b { } = P a X b { } ( )d b a = f x x = P a X b { } { } X a = 是不可能事件 = = P X a { } 0. 若 X为离散型随机变量, 概率为0的事件不一定是不可能事件。 同样,概率为1的事件也不一定是必然事件。 说明:

例1.设随机变量X具有概率密度 kx, 0≤x<3, -2- 3≤x≤4, 0, 其他. ()确定常数k; Q)求X的分布画数:O)求P1<Xs》 解()由∫fx)dx=l, 得心cdx+-之ar=山,解之得k=君
, 0 3, ( ) 2 , 3 4, 2 0, . 7 (1) ; (2) ; (3) {1 . 1 } 2 . X kx x x f x x k X P X = − 设随机变量 具有概率密度 其他 确定常数 求 的分布函数 求 例 解 (1) ( )d 1, f x x − = 由 3 4 0 3 d (2 )d 1, 2 x kx x x + − = 得 1 . 6 解之得 k =