
第三讲线性变换矩阵及其对角化 ·线性变换的矩阵表示 冬线性变换及矩阵的值域和核 冬特征值和特征向量 冬矩阵对角化的充要条件 冬内积空间 lexu@mail.xidian.edu.cn 矩阵论● 6
第 讲三 线性变换矩阵及其对角化 线性变换的矩阵表示 线性变换及矩阵的值域和核 特征值和特征向量 矩阵对角化的充要条件 内积空间 lexu@mail.xidian.edu.cn 矩 阵 论 6

线性变换的矩阵表示 线性变换用矩阵表示,将抽象的线性变换 转化为具体的矩阵形式 ■设T是线性空间Vn的一个线性变换 {1,水2,,xn}是y的的一个基 ·x∈V",存在唯一的坐标表示 Tx=T(51x1+52x2+…+5nxn) 51 =[T(x1,x2,…,xn) 52 = 5x1+52x2+…+5nx,5n」 5n」 lexu@mail.xidian.edu.cn 矩阵论
线性变换的矩阵表示 线性变换用矩阵表示,将抽象的线性变换 转化为具体的矩阵形式 设 T是线性空间 V n的 个线性变换 的 一个线性变换 是V x 1 , x 2 , , x n n的的一个基 ,存在唯一的坐标表示 n x V 1 x x x x x x x 2 1 ( ) 1 1 2 2 n Tx T x x x n n T x x x 2 1 2 ( , , , ) n x x x x x x x n n n 1 2 1 1 2 2 , , , n lexu @mail.xidian.edu.cn 矩 阵 论 7
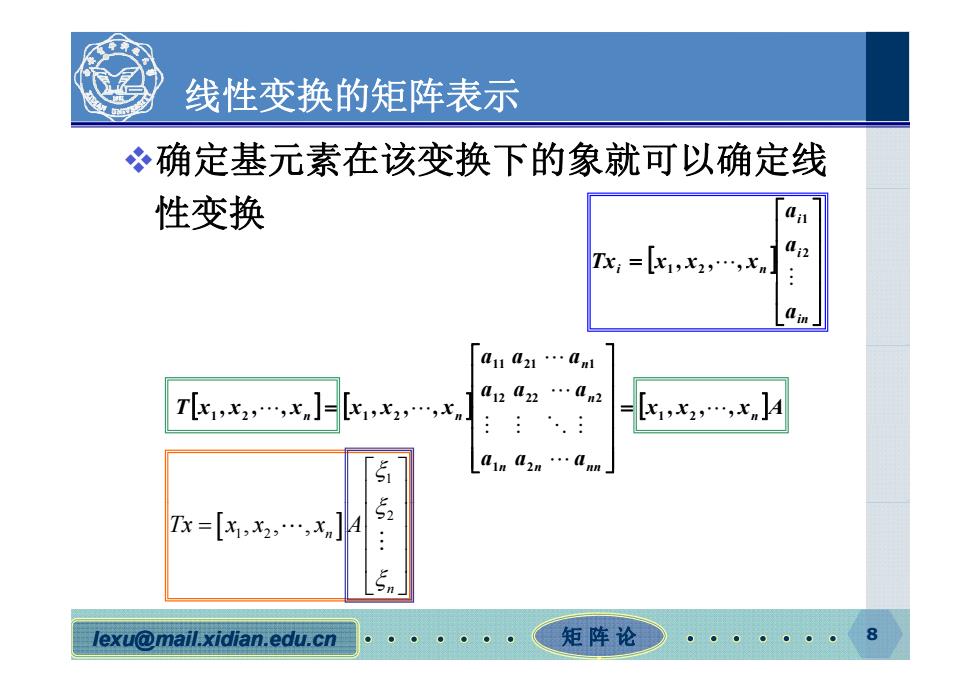
线性变换的矩阵表示 确定基元素在该变换下的象就可以确定线 性变换 Tx,=[x1,2,…,x a11a21…aml Tx1x2,…,xn]= 012022…2 X1,X2,,xn 1,x2,…,nA Tx=[x1,2,…,Xn A 55: lexu@mail.xidian.edu.cn 矩阵论 8
线性变换的矩阵表示 确定基元素在该变换下的象就可以确定线 性变换 i i i n a a Tx x x x 2 1 1 2 , , , in i n a Tx x x x 1 2 , , , x x x A a a a a a a T x x x x x x n n n n n , , , , , , , , , 1 2 12 22 2 11 21 1 1 2 1 2 a a a 1n 2 n nn 1 2 1 2 ,,, Tx x x x A n lexu @mail.xidian.edu.cn 矩 阵 论 8 n
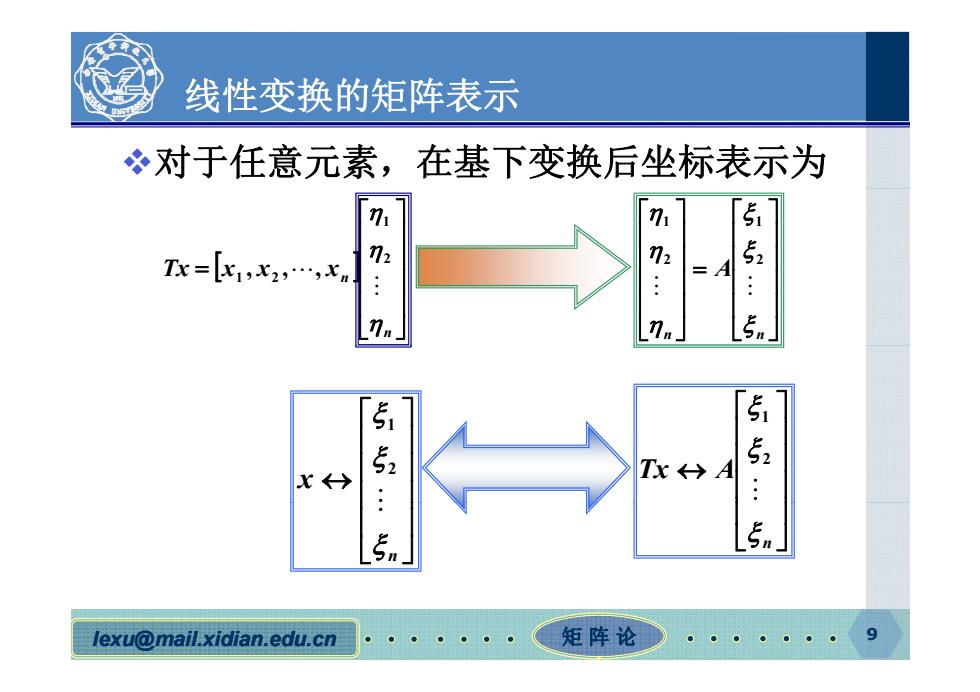
线性变换的矩阵表示 对于任意元素,在基下变换后坐标表示为 n n Tx=[x1,x2,,xn 72 72 5 .: y nn」 5n」 X←→ Tx←→ A 5.5: n lexu@mail.xidian.edu.cn 矩阵论D
线性变换的矩阵表示 对于任意元素,在基下变换后坐标表示为 Tx x x x 2 1 A 2 1 2 1 n n Tx x x x 1 , 2 ,, n n A 1 1 x 2 1 Tx A 2 n n lexu @mail.xidian.edu.cn 矩 阵 论 9

线性变换的矩阵表示 定义:把A称为在基{c1,x2,,xn}下的矩阵 定理: ■设{x1,x2,,xn}是V"的一个基,T1、T2在该基 下的矩阵分别为A、B。则有 匹+Tx1,x2,…,xn]=1,x2,…,xnA+B) kT,KkA) (TT)x2,x2,xKAB) T-[x1,x2,…,xn]=[1,x2,…,xn]A lexu@mail.xidian.edu.cn 矩阵论 10
线性变换的矩阵表示 定义:把 A称为在基 下的矩阵 x 1 , x 2 , , x n 定理: 设 是 V n的 个基 一 , T1 、 T2在该基 下的矩阵分别为 A 、B 。则有 x 1 , x 2 ,, x n ( ) , , , , , , ( ) T1 T2 x 1 x 2 x n x 1 x 2 x n A B , , , , , , ( ) 1 1 2 1 2 kT x x x n x x x n kA ( T T ) , , , , , , (AB ) T1 T2 x 1 x 2 x n x 1 x 2 x n AB 1 1 2 1 2 1 , , , , , , T x x x n x x x n A lexu @mail.xidian.edu.cn 矩 阵 论 10 1 2 1 2 , , , , , , n n