
例4.试建立顶点在原点,旋转轴为z轴,半顶角为α的圆面方程解:在yoz面上直线L的方程为Lz =ycotαM(0,y,z)绕轴旋转时,圆锥面的方程为z =±/x? + y? cotα令 a= cotα两边平方x=α2(x2 +y2)
例4. 试建立顶点在原点, 旋转轴为z 轴, 半顶角为 的圆锥面方程. 解: 在yoz面上直线L 的方程为 z = y cot 绕z 轴旋转时,圆锥面的方程为 cot 2 2 z = x + y ( ) 2 2 2 2 z = a x + y 令 a = cot x y z 两边平方 L M(0, y,z)
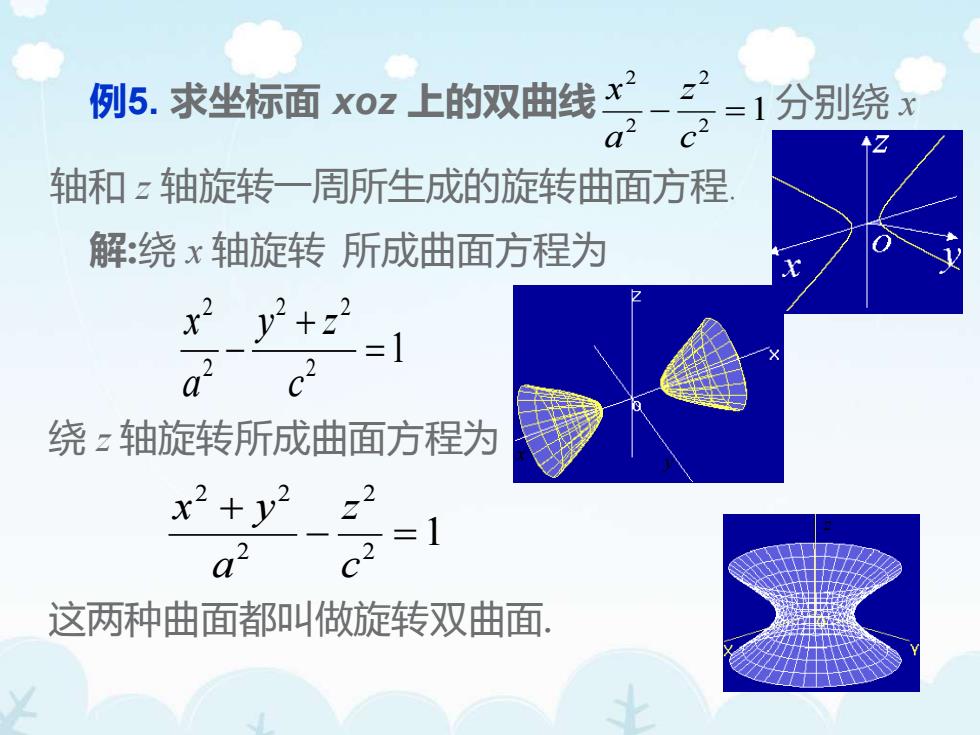
例5.求坐标面xoz上的双曲线=1分别绕12轴和z轴旋转一周所生成的旋转曲面方程解:绕x轴旋转所成曲面方程为x212+z二2o绕乙轴旋转所成曲面方程为x? +y2722a福这两种曲面都叫做旋转双曲面
x y 例5. 求坐标面 xoz 上的双曲线 1 2 2 2 2 − = c z a x 分别绕 x 轴和 z 轴旋转一周所生成的旋转曲面方程. 解:绕 x 轴旋转 1 2 2 2 2 2 = + − c y z a x 绕 z 轴旋转 1 2 2 2 2 2 − = + c z a x y 这两种曲面都叫做旋转双曲面. 所成曲面方程为 所成曲面方程为 z
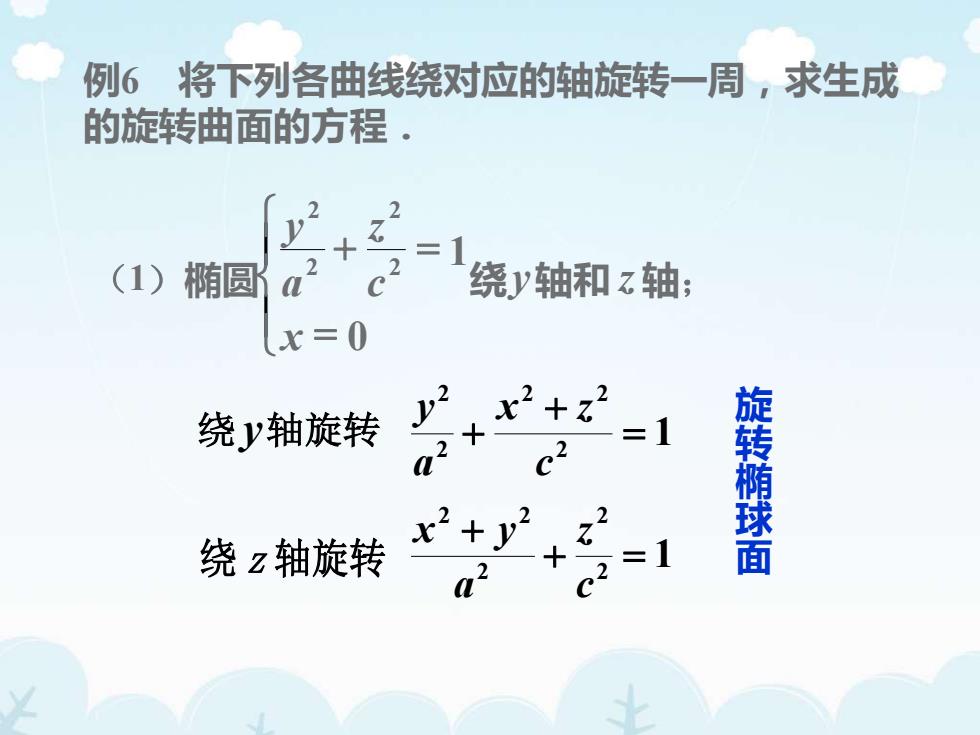
例6将下列各曲线绕对应的轴旋转一周,求生成的旋转曲面的方程·2N+2(1)椭圆绕轴和z轴aCx=0旋转椭球面绕y轴旋转2N绕z轴旋转
例6 将下列各曲线绕对应的轴旋转一周,求生成 的旋转曲面的方程. 旋 转 椭 球 面 绕 y轴旋转 1 2 2 2 2 2 = + + c x z a y 1 2 2 2 2 2 + = + c z a x y (1)椭圆 = + = 0 1 2 2 2 2 x c z a y 绕y轴和 z 轴; 绕 z 轴旋转

2pz绕z轴;(2)抛物线lx=0x2 + y2=2pz旋转抛物面SCUMATHZUO
x y 2 pz 2 2 + = 旋转抛物面 (2)抛物线 = = 0 2 2 x y pz 绕z轴;
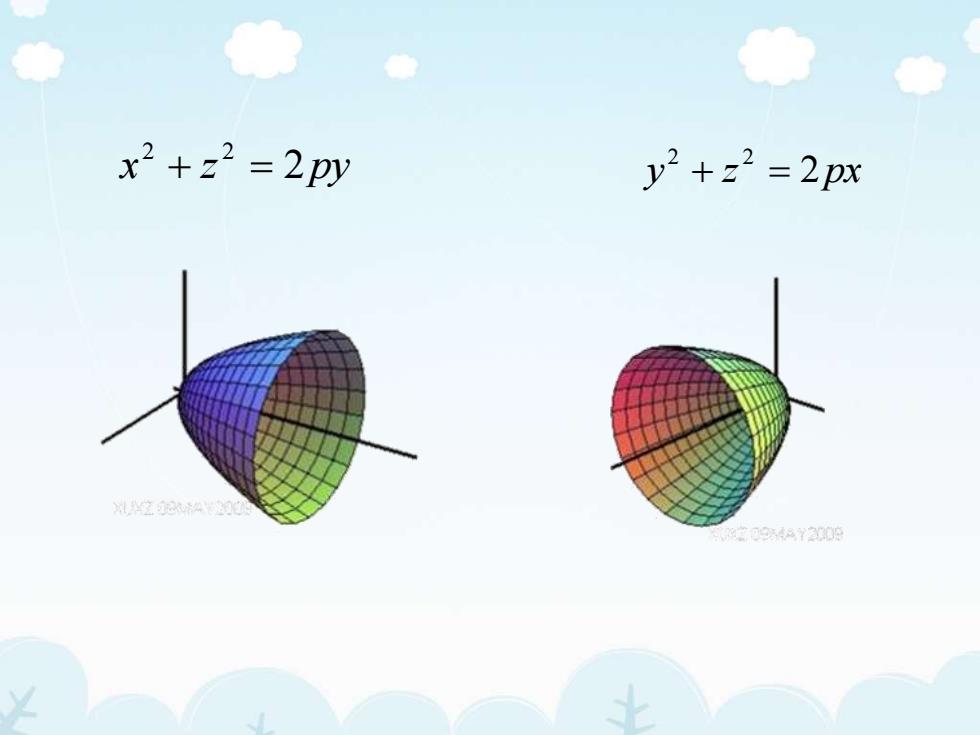
x? +z? = 2pyy? +z? = 2px904AY2009
x z 2py 2 2 + = y z 2px 2 2 + =