
三、柱面引例.分析方程2+2=R2M表示怎样的曲面CO!解:在xoy面上,x+y2=R?表示圆CyM在圆C上任取一点M,(x,y,0),过此点作x平行z轴的直线l,对任意z,点M(x,y,z)的坐标也满足方程 x2+y2=R2故在空间中x+2=R2表示圆柱面
x y 三、柱面 z 引例. 分析方程 表示怎样的曲面 . 的坐标也满足方程 2 2 2 x + y = R 解:在 xoy 面上, 表示圆C, 2 2 2 x + y = R 2 2 2 x + y = R 故在空间中 2 2 2 x + y = R 过此点作 平行 z 轴的直线 l , 对任意 z , 表示圆柱面. C o 在圆C上任取一点 ( , ,0), 1 M x y l M M1 点M(x, y,z)

定义3.平行定直线并沿定曲线C移动的直线1形成C叫做准线【叫做母线的轨迹叫做柱面Z。y2=2x表示抛物柱面母线平行于z轴0准线为xoy面上的抛物线x221x2=1表示母线平行于十262aZ轴的椭圆柱面-=0表示母线平行于V轴的平面yxx(且z轴在平面上)
x y z x y z o l 定义3. 平行定直线并沿定曲线 C 移动的直线 l 形成 的轨迹叫做柱面. • 表示抛物柱面, 母线平行于 z 轴; 准线为xoy 面上的抛物线. z 轴的椭圆柱面. y 2x 2 = 1 2 2 2 2 + = b y a x • z 轴的平面. • x − y = 0 表示母线平行于 C (且 z 轴在平面上) 表示母线平行于 C 叫做准线, l 叫做母线. x y z o o
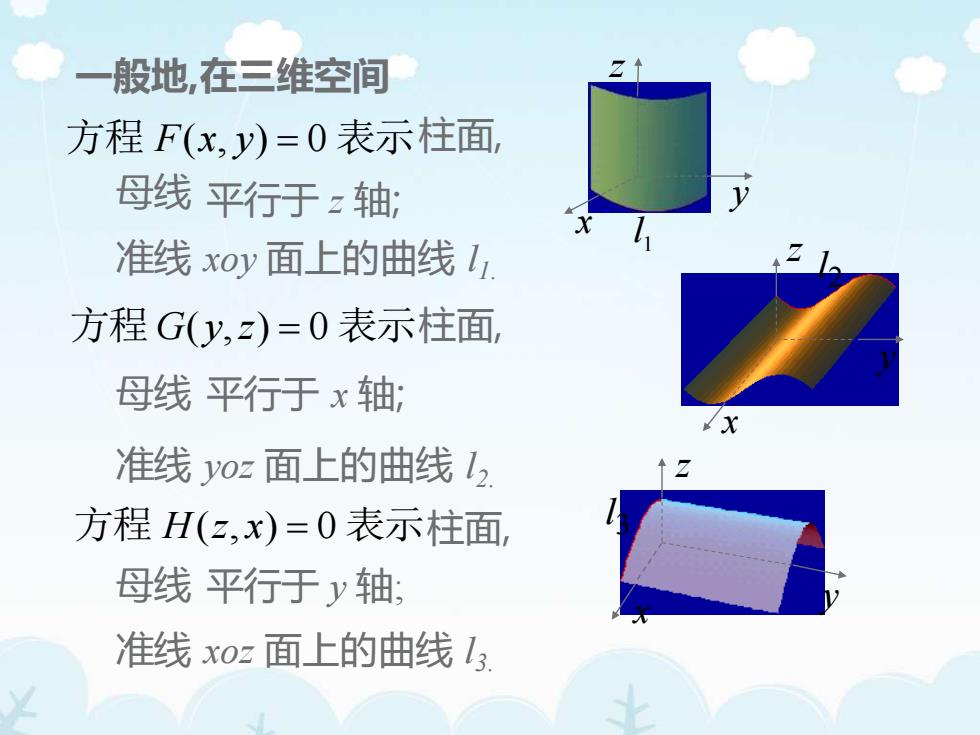
一般地,在三维空间方程 F(x,y)=0 表示柱面母线平行于z轴X准线xoy面上的曲线l方程 G(y,z)=0 表示柱面)母线平行于x轴准线yoz面上的曲线12Z方程 H(z,x)= 0 表示柱面母线平行于轴准线xoz面上的曲线13
x z y 2 l 一般地,在三维空间 柱面, 柱面, 平行于 x 轴; 平行于 y 轴; 平行于 z 轴; 准线 xoz 面上的曲线 l3. 母线 柱面, 准线 xoy 面上的曲线 l1. 母线 准线 yoz 面上的曲线 l2. 母线 方程 F(x, y) = 0 表示 方程 G( y,z) = 0 表示 方程 H(z, x) = 0 表示 x y z 3 l x y z 1 l

四、二次曲面三元二次方程Ax?+By?+Cz?+Dxy+Eyx +Fzx+Gx + Hy + Iz + J = 0(二次项系数不全为0)其基本类型有的图形通常为二次曲面椭球面、锥面抛物面、双曲面、适当选取直角坐标系可得它们的标准方程,下面仅就几种常见标准型的特点进行介绍研究二次曲面特性的基本方法:截痕法
四、二次曲面 三元二次方程 适当选取直角坐标系可得它们的标准方程,下面仅 就几种常见标准型的特点进行介绍 . 研究二次曲面特性的基本方法: 截痕法 其基本类型有: 椭球面、抛物面、双曲面、锥面 的图形通常为二次曲面. Ax + By +Cz + Dxy + Eyx + Fzx 2 2 2 + Gx + Hy + Iz + J = 0 (二次项系数不全为 0 )