
例3. 研究方程x2+y2+z2-2x+4y=0表示怎样的曲面。解:配方得(x-1)+(y+2)2+z2=5此方程表示:球心为 Mo(1,-2,0)半径为√5的球面如下形式的三元二次方程(A+0)说明:A(x? + y? + z2)+ Dx + Ey+ Fz +G = 0都可通过配方研究它的图形.其图形可能是一个球面,或点,或虚轨迹
例3. 研究方程 2 4 0 2 2 2 x + y + z − x + y = 解: 配方得 5 (1, 2, 0), 此方程表示: M0 − 说明: 如下形式的三元二次方程 ( A≠ 0 ) 都可通过配方研究它的图形. 其图形可能是 的曲面. 表示怎样 半径为 的球面. ( ) 0 2 2 2 A x + y + z + Dx + Ey + Fz + G = 球心为 一个球面 , 或点 , 或虚轨迹. ( 1) ( 2) 5 2 2 2 x − + y + + z =

两个基本问题:(1)已知一曲面作为点的几何轨迹时求曲面方程(2)已知方程时,研究它所表示的几何形状(必要时需作图)作为基本问题(1)的例子,我们讨论旋转曲面:作为基本问题(2)的例子,我们讨论柱面:最后对二次曲面的讨论,我们也看作基本问题(2)的例子
两个基本问题 : (1) 已知一曲面作为点的几何轨迹时, 求曲面方程. (2) 已知方程时 , 研究它所表示的几何形状 ( 必要时需作图 ). 作为基本问题(1)的例子,我们讨论旋转曲面;作为 基本问题(2)的例子,我们讨论柱面;最后对二次曲 面的讨论,我们也看作基本问题(2)的例子
二、旋转曲面定义2。一条平面曲线绕其平面上一条定直线旋转一周所形成的曲面叫做旋转曲面该定直线称为旋转轴.平面曲线称为母线例如:
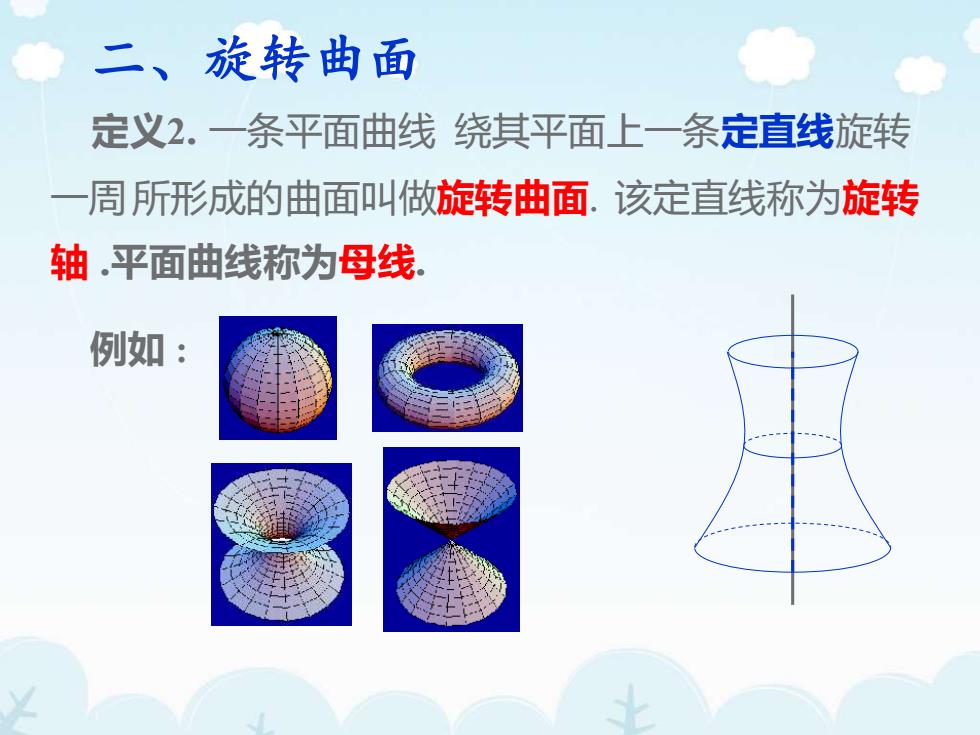
定义2. 一条平面曲线 二、旋转曲面 绕其平面上一条定直线旋转 一周所形成的曲面叫做旋转曲面. 该定直线称为旋转 轴 .平面曲线称为母线. 例如 :

建立yoz面上曲线C绕z轴旋转所成曲面的方程给定yoz面上曲线C:f(y,z)=0Z若点 Mi(0,J1,z1)EC,则有f(y1,z1)= 0CM,(0, y1,z1)-当绕轴旋转时,该点转到M(x,y,z),M(x,y,z),则有0x? +y? =[y1yz = Z12x故旋转曲面方程为f(±/x2 +y2,z)=0
建立yoz面上曲线C 绕 z 轴旋转所成曲面的方程: 故旋转曲面方程为 M(x, y,z) , 当绕 z 轴旋转时, f (y1 ,z1 ) = 0 (0, , ) , 若点 M1 y1 z1 C 给定 yoz 面上曲线 C: (0, , ) 1 1 1 M y z M (x, y,z) 1 2 2 1 z = z , x + y = y 则有 ( , ) 0 2 2 f x + y z = 则有 该点转到 f (y,z) = 0 o z y x C

思考:当曲线C绕y轴旋转时,方程如何?C: f(y,z)= 0Z福+f(y, ±Vx? +z?)=0小结:平面曲线绕某轴旋转,轴坐标变量不变而将曲线方程中的另一变量改写成该变量与第三个变量的平方和的正负平方根
思考:当曲线 C 绕 y 轴旋转时,方程如何? C : f (y,z) = 0 o y x z ( , ) 0 2 2 f y x + z = 小结:平面曲线绕某轴旋转,轴坐标变量不变, 而将曲线方程中的另一变量改写成该变量与第三 个变量的平方和的正负平方根