性质4(行列式的初等变换)(2)行列式的某一行元素都乘以同一个数k后,加到另一行的对应元素上,行列式的值不变;证明:ana,a,aa,4ailaa,aidin0daαinanlanaa.a.a4值为0
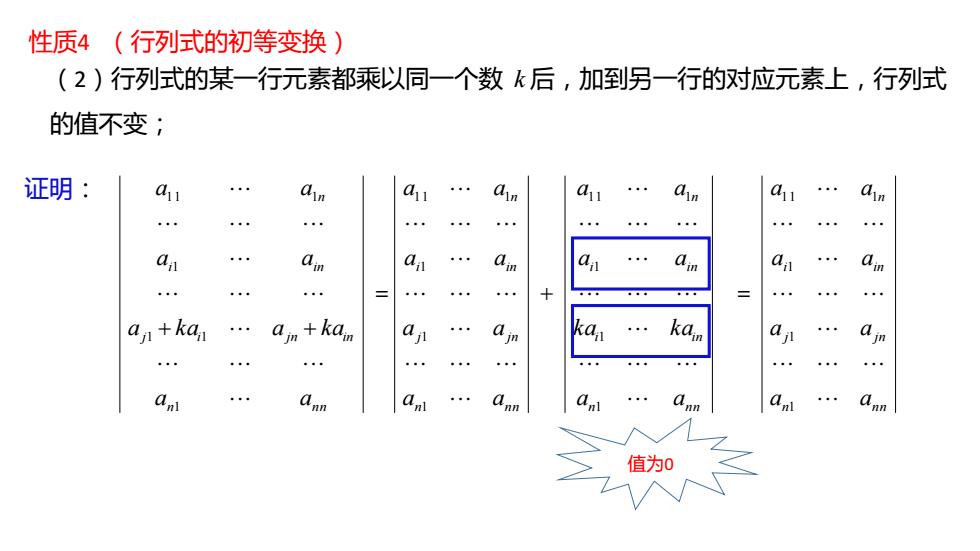
性质4 (行列式的初等变换) (2)行列式的某一行元素都乘以同一个数 k 后,加到另一行的对应元素上,行列式 的值不变; 证明: 1 1 1 1 1 1 1 n n n j i jn in i in n a a a k a a k a a a a a 1 1 1 1 1 1 1 1 1 1 1 1 n n n i in i in n n n n j jn i in n a a k a k a a a a a a a a a a a a a 1 1 1 1 1 1 n n n j jn i in n a a a a a a a a 值为0

性质4(行列式的初等变换)(3)互换行列式的两行元素,行列式变号。证明aainainailajiainajnajlajlajn-ailain+yailaina,+a+a;+9+ainanlananlannanlann
性质4 (行列式的初等变换) (3)互换行列式的两行元素,行列式变号。 证明: 1 1 1 1 1 1 n n n i in j jn n a a a a a a a a 1 1 1 1 1 1 1 n n n i j in jn j jn n i j a a a a a a a a a a r r 1 1 1 1 1 1 1 n n n i j in jn i in n j i a a a a a a a a a a r r

aauaindndin0aiain-D+aaInanlannaakrkr +rj行列式的初等变换rr
1 1 1 1 1 1 n n n j jn i in n i j a a a a a a a a r r 1 1 1 1 1 1 n n n j jn i in n a a a a a a a a D 行列式的初等变换 i j i j i r r kr r kr

6a1-2ai2-8aj3anai3ai2例3 设 D==2,计算行列式_3a214a23a21a22a23a22-3a314a33a31a32a33a32a, +b,a, +b,a, +b,aia2a3例4证明=2bsbib2b+cib, +C2b, +C3ciC2C3C3 +a3Ci+ac,+a
例3 设 2 ,计算行列式 3 1 3 2 3 3 2 1 2 2 2 3 1 1 1 2 1 3 a a a a a a a a a D 3 4 3 4 6 2 8 3 1 3 2 3 3 2 1 2 2 2 3 1 1 1 2 1 3 a a a a a a a a a 例4 证明 1 1 2 2 3 3 1 2 3 1 1 2 2 3 3 1 2 3 1 1 2 2 3 3 1 2 3 2 a b a b a b a a a b c b c b c b b b c a c a c a c c c

#初等矩阵的行列式det(E,A) = -det A = det E., - det Adet E, =-det I =-1det E,(c) = cdet I = cdet (E,(c)A) = cdet A = det (E,(c)· det Adet E,(c)= det I = 1det (E, (c)A) = det A = det (E, (c) · det A结论(1)对任一初等矩阵E,det (EA)= det E-det A(2)对初等矩阵E,E2,EdetEE..EA)=detEdetE,.detEdetA(3)对任一初等矩阵E,det ET = det E
# 初等矩阵的行列式 det Eij det I 1 E c c I c det i ( ) det det Eij(c) det I 1 det(EijA) det A det Eij det A det (Ei (c)A) cdet A det (Ei (c)det A det (Eij(c)A) det A det (Eij(c)det A (1)对任一初等矩阵 E, det (EA) det Edet A (2)对初等矩阵 E1 ,E2 , ,Es , det(E1 E2 Es A) det E1 det E2 . det Es det A 结论 (3)对任一初等矩阵 E, E E T det det