
第五节 极限运算法则 一、无穷小运算法则 二、 极限的四则运算法则 三、复合函数的极限运算法则
二、 极限的四则运算法则 三、 复合函数的极限运算法则 一 、无穷小运算法则 第五节 极限运算法则

一、无穷小运算法则 定理1.有限个无穷小的和还是无穷小 证:考虑两个无穷小的和.设lim&=0,limB=0, x→x0 x→x0 Ve>0,381>0,当0<x-xo<6时,有a<号 382>0,当0<x-x0<62时,有B< 取6=min{6,d2),则当0<x-xo<6时,有 a+Bsa+B<号+号=8 因此 lim(a+β)=0. x→x0 这说明当x→xo时,a+B为无穷小量
min 1 , 2 , 时, 有 一、 无穷小运算法则 定理1. 有限个无穷小的和还是无穷小 . 证: 考虑两个无穷小的和 . 设 0 , 当 时 , 有 当 时 , 有 取 则当 0 0 x x 2 2 因此 这说明当 时, 为无穷小量

类似可证:有限个无穷小之和仍为无穷小 说明:无限个无穷小之和不一定是无穷小 例如, 1.1 lim nn
说明: 无限个无穷小之和不一定是无穷小 ! 例如, 1 1 1 lim n n n n 1 类似可证: 有限个无穷小之和仍为无穷小

定理2,有界函数与无穷小的乘积是无穷小 证:设Vx∈U(xo,d),u≤M 又设lima=0,即6>0,382>0,当x∈U(xo,82) x→X0 时,有a 取6=min{61,62},则当xeU(xo,6)时,就有 ua=ua≤M·&=& 故lim ua=0,即uc是x→xo时的无穷小 X→x0 推论1,常数与无穷小的乘积是无穷小 推论2,有限个无穷小的乘积是无穷小
定理2 . 有界函数与无穷小的乘积是无穷小 . 证: 设 u M 又设 lim 0, 0 x x 即 0 , 当 时, 有 M 取 min , , 1 2 则当 ( , ) 0 x U x 时 , 就有 u u M M 故 即 是 时的无穷小 . 推论 1 . 常数与无穷小的乘积是无穷小 . 推论 2 . 有限个无穷小的乘积是无穷小
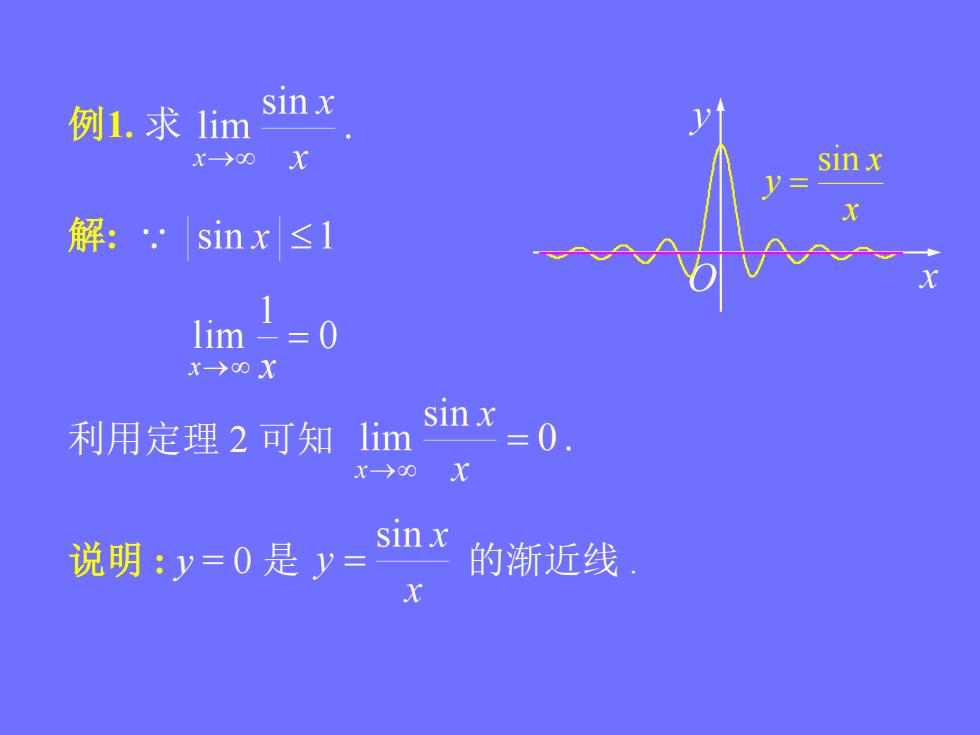
例1,求lim sinx x→00X sinx V= 解:sinx≤1 1im=0 X→0X sinx 利用定理2可知lim =0 x-→00 说明:y=0是y= sinx 的渐近线 x
例1. 求 解: 0 1 lim x x 利用定理 2 可知 说明 : y = 0 是 的渐近线 . x x y sin