
第九节 连续虽数的运算与 初等盈数的连疾性 一、连续函数的运算法则 二、初等函数的连续性
一、连续函数的运算法则 第九节 二、初等函数的连续性 连续函数的运算与 初等函数的连续性

一、连续函数的运算法则 定理1.在某点连续的有限个函数经有限次和,差,积, 商(分母不为0)运算,结果仍是一个在该点连续的函数. (利用极限的四则运算法则证明) 例如,sinx,cosx连续 →tanx,cotx在其定义域内连续 定理2.连续单调递增函数的反函数也连续单调递增 (递减) (递减) (证明略 y sinx 例如,y=sinx在[-受,]上连续单调递增, arcsin x 其反函数y=arcsinx在[l,1]上也连续单调 递增
定理2. 连续单调递增函数的反函数也连续单调递增. 在其定义域内连续 一、连续函数的运算法则 定理1. 在某点连续的有限个函数经有限次和 , 差 , 积 , ( 利用极限的四则运算法则证明) 商(分母不为 0) 运算, 结果仍是一个在该点连续的函数 . 例如, 例如, y sin x 在 上连续单调递增, 其反函数 y arcsin x (递减) (证明略) 在[1, 1]上也连续单调 (递减) 1 1 O x y 2 π 2 π 递增. sin x arcsin x

又如,y=e在(-oo,+oo)上连续 v=e 单调递增,其反函数y=nx在 y=Inx (0,+0)上也连续单调递增 定理3.若limg(x)=,函数f(u)在点4,连续 x→X 则有1imf几g(x)]=f(4)=f[limg(x] 注:1.定理的条件:内层函数有极限,外层函数 在极限值点处连续。 2将x→x,换成x→o可得类似的定理
在 上连续 其反函数 在 上也连续单调递增. 又如, x y O y ln x e x y 1 1 单调 递增, 定理3. 0 0 0 0 0 0 lim ( ) , ( ) , lim [ ( )] ( ) [lim ( )]. 若 函数 在点 连续 则有 x x x x x x g x u f u u f g x f u f g x 注: 1.定理的条件:内层函数有极限,外层函数 在极限值点处连续. 0 2.将x x x 换成 可得类似的定理

又如,y=e在(-o,+oo)上连续 =e 单调递增,其反函数y=nx在 y=Inx (0,+o0)上也连续单调递增, 定理3.若limg(x)=,函数f(u)在点,连续 则有Iimf几g(x】=f(4)=f[lim g(x] X->X x->xo 意义: 在定理的条件下,极限符号可以与函数符号 互换,即极限号可以穿过外层函数符号直接 取在内层
在 上连续 其反函数 在 上也连续单调递增. 又如, x y O y ln x e x y 1 1 单调 递增, 定理3. 0 0 0 0 0 0 lim ( ) , ( ) , lim [ ( )] ( ) [lim ( )]. 若 函数 在点 连续 则有 x x x x x x g x u f u u f g x f u f g x 意义: 在定理的条件下,极限符号可以与函数符号 互换,即极限号可以穿过外层函数符号直接 取在内层
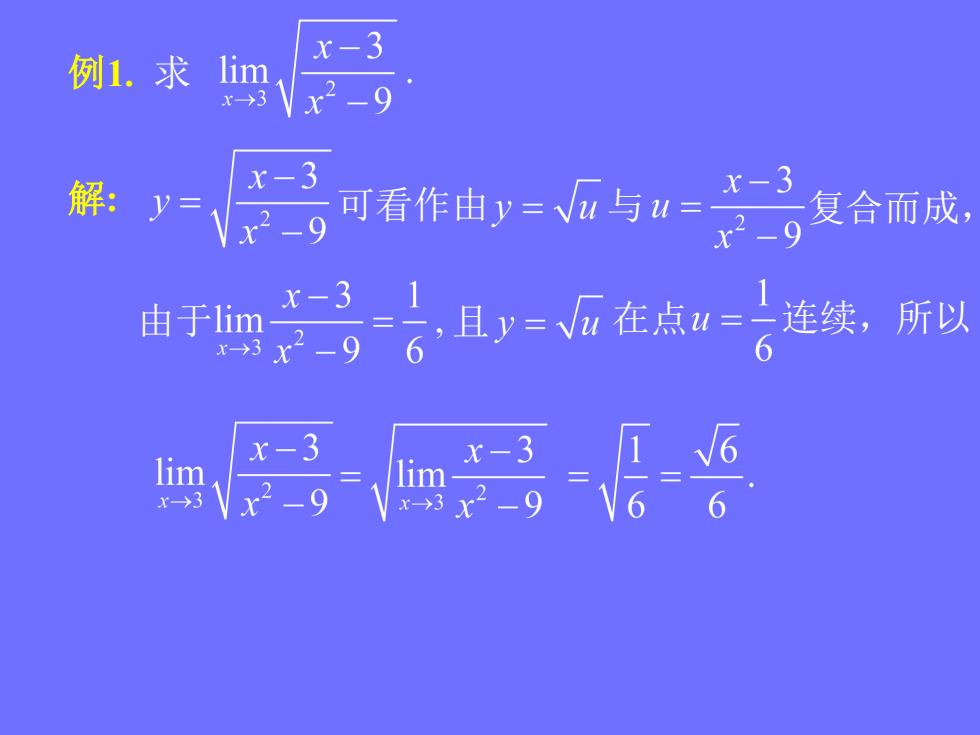
x-3 例1.求 lim x2-9 解: X-3 y- x2-9 可看作由y=G与u=x-3 x2二9复合而成, X-3 由于lim x2-9 。1y=面在点=运统, 所以 x-3 lim x→3 x2-9
例1. 求 解: 可看作由 与 复合而成, 由于 且 在点 连续,所以