
第一章 温数与极限 习题课
第一章 函数与极限 习 题 课
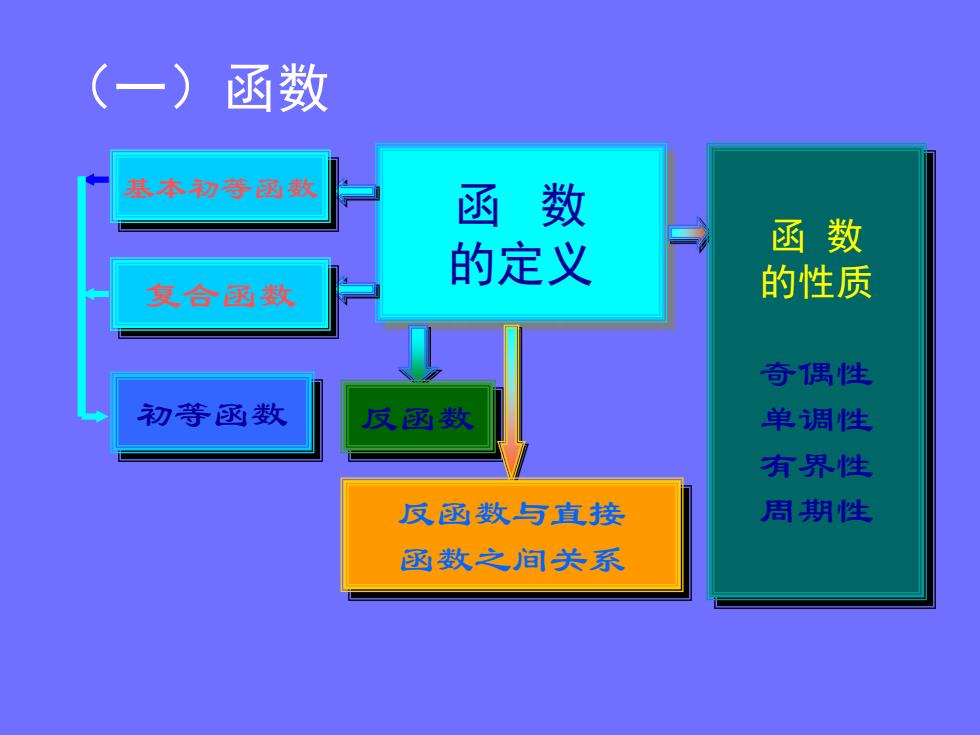
(一)函数 基本初等的款 函数 函数 的定义 复合函数 的性质 奇偶性 初等函数 反函数 单调性 有界性 反函数与与直接 周期性 函数之间关系
函 数 的定义 函 数 的性质 奇偶性 单调性 有界性 周期性 反函数 反函数与直接 函数之间关系 基本初等函数 复合函数 初等函数 (一)函数
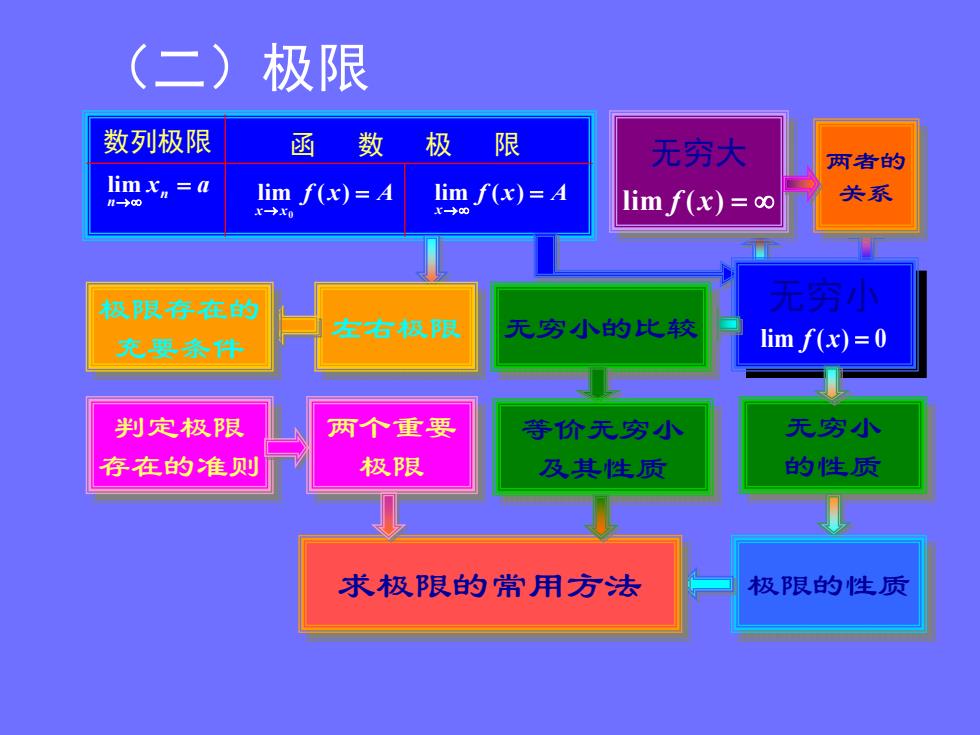
(二) 极限 数列极限 函数 极限 无穷大 两者的 lim x a lim f(x)=A lim f(x)=A 关系 r→rn →0 limf(x)=∞ 极限存在的 无穷小 左右极限 无穷小的比较 充要条件 lim f(x)=0 判定极限 两个重要 等价无穷小 无穷小 存在的准则 极限 及其性质 的性质 求极限的常用方法 极限的性质
数列极限 函 数 极 限 xn a n lim f x A x f x A lim ( ) x x lim ( ) 0 左右极限 极限存在的 充要条件 无穷大 lim f ( x) 两者的 关系 无穷小 的性质 求极限的常用方法 极限的性质 无穷小 lim f (x) 0 判定极限 存在的准则 两个重要 极限 无穷小的比较 等价无穷小 及其性质 (二)极限
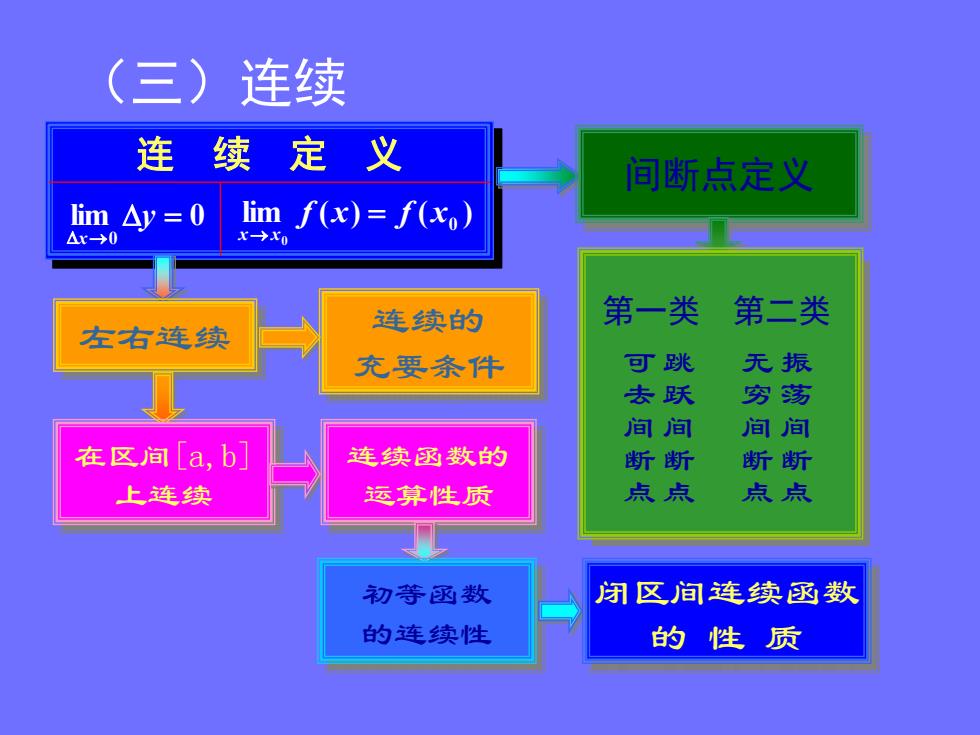
(三)连续 连续定义 间断点定义 Iim△y=0 1imf(x)=f(x,) △x-→0 x->x0 第一类 第二类 左右连续 连续的 充要条件 可跳 无振 去跃 穷荡 间间 间间 在区间[a,b 连续函数的 断断 断断 上连续 运算性质 点点 点点 初等函数 闭区间连续函数 的连续生 的性质
(三)连续 连 续 定 义 lim 0 0 y x lim ( ) ( ) 0 0 f x f x x x 连 续 定 义 lim 0 0 y x lim ( ) ( ) 0 0 f x f x x x 左右连续 连续的 充要条件 间断点定义 振 荡 间 断 点 无 穷 间 断 点 跳 跃 间 断 点 可 去 间 断 点 第一类 第二类 在区间[a,b] 上连续 连续函数的 运算性质 初等函数 的连续性 闭区间连续函数 的 性 质

1、两个重要极限 sinx 1 lim sin (x) lim =1 x→>0 p(x)→0 o(x) im1+)》产=e→,m(1+g)w=e c->o 0(x)-→o0 或1im(l+x)=e→lim(1+o(x)o=e (X)-
1、 两个重要极限 1 0 lim(1 ) e 或 x x x