
第二节 岛数的求导法则 一、 四则运算求导法则 二、反函数的求导法则 三、复合函数求导法则 四、初等函数的求导问题
第二节 二、反函数的求导法则 三、复合函数求导法则 四、初等函数的求导问题 一、四则运算求导法则 函数的求导法则
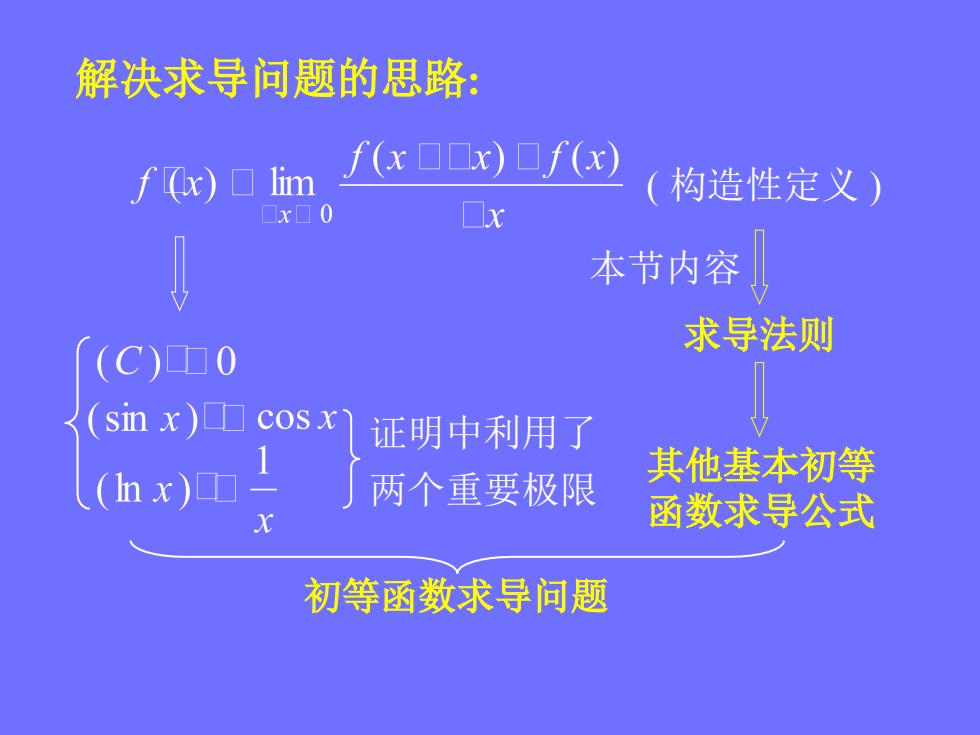
解决求导问题的思路: fx)▣lim f(x口口x)口f(x) 构造性定义) 口x▣0 ■ 本节内容 求导法则 (C)中0 (sinx)▣ coSx 证明中利用了 (nx)西 其他基本初等 两个重要极限 函数求导公式 初等函数求导问题
解决求导问题的思路: ( 构造性定义 ) 求导法则 其他基本初等 函数求导公式 证明中利用了 两个重要极限 初等函数求导问题 本节内容

一、四则运算求导法则 定理1.函数口(x)及v□v(x)都在点x可导 →(x)及v(x)的和、差、积、商(除分母 为O的点外)都在点x可导,且 (1)[(x)☐v(x)]Dux)口vCx) (2)[u(x)v(x)]☐ux)v(x)☐u(x)vx) (3 gu(四aGD(wp (v(x)☐0) 目v(x)E v-(x) 下面分三部分加以证明,并同时给出相应的推论和 例题
一、四则运算求导法则 定理1. 的和、差、积、商 (除分母 为 0的点外) 都在点 x 可导, 且 下面分三部分加以证明, 并同时给出相应的推论和 例题

(1)(w☐v)Du☐v0 证:设f(x)口u(x)☐v(x),则 fqx)口lim f(x☐h)☐f(x) h▣0 h lim [u(x☐h)☐v(xDh)]□[u(x)☐v(x)] h☐0 h u(x☐h)☐u(x) ▣lim lim v(x☐h)☐v(x) h▣0 n h▣0 h 口ux)☐vx) 故结论成立, 此法则可推广到任意有限项的情形.例如, (u☐y☐P)DDv☐
此法则可推广到任意有限项的情形. 证: 设 则 故结论成立. 例如

(2) (uy)☐更u☐uy 证:设f(x)口u(x)v(x),则有 fx)☐lim f(x□h)▣f(x) u(x☐h)v(x☐h)☐u(x)v(x) ▣lim h▣0 h h▣0 ▣lim 2(x☐h)☐u(x) 0日 (xCh)☐(x)'x☐h(xU n ☐ux)v(x)☐u(x)vx) 故结论成立 推论:1)(Cu)工Cu[(C为常数) 2)(1w)工u☐1v☑☐1w[ 3)(loga x)口 nx Ina xlna
(2) 证: 设 则有 故结论成立. 推论: ( C为常数 )