
第一为 映射与画数 一、映射 二、函数
二、 函数 一 、映射 第一节 映射与函数
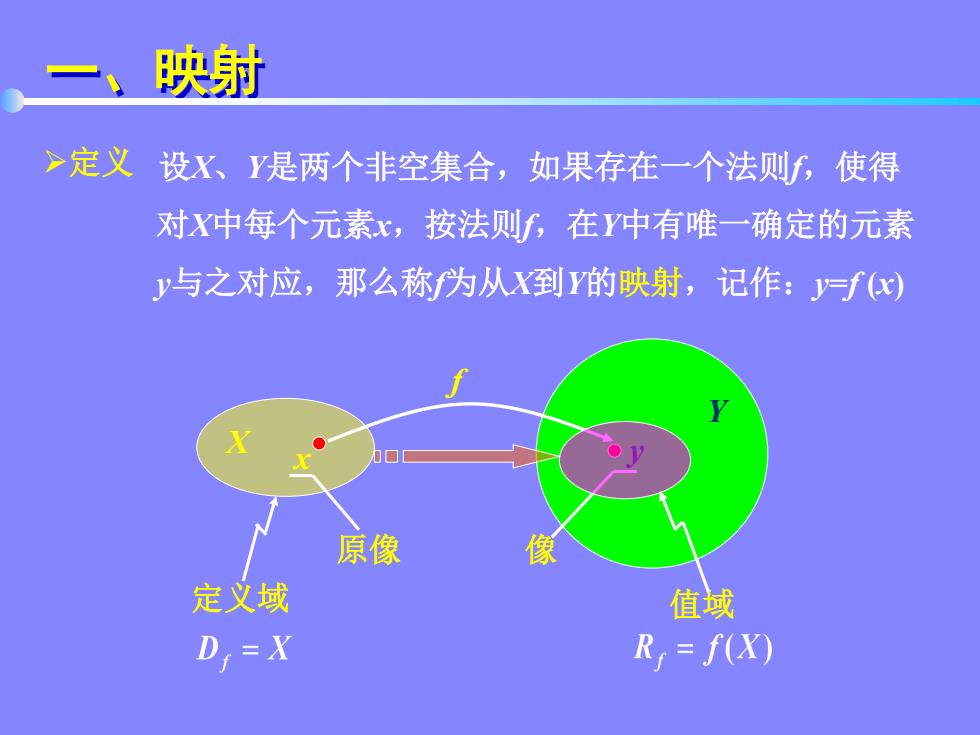
映射 >定义设X、Y是两个非空集合,如果存在一个法则f,使得 对X中每个元素x,按法则f,在Y中有唯一确定的元素 y与之对应,那么称为从X到的映射,记作:J=f) 原像 像 定义域 值域 Di=X R,=f(X)
一、映射 定义 设X、Y是两个非空集合,如果存在一个法则f,使得 对X中每个元素x,按法则f,在Y中有唯一确定的元素 y与之对应,那么称f为从X到Y的映射,记作:y=f (x) X Y x y f 原像 像 定义域 值域
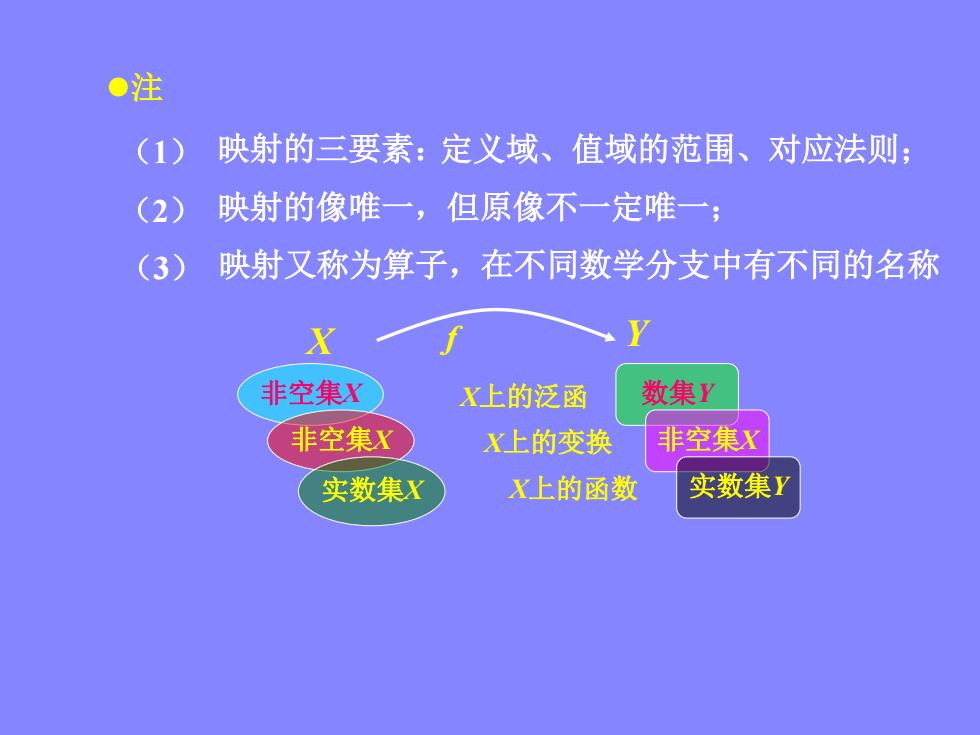
●注 (1) 映射的三要素:定义域、值域的范围、对应法则; (2) 映射的像唯一,但原像不一定唯一; (3) 映射又称为算子,在不同数学分支中有不同的名称 X 非空集X X上的泛函 数集Y 非空集X X上的变换 非空集X 实数集X X上的函数 实数集Y
注 (1) 映射的三要素:定义域、值域的范围、对应法则; (2) 映射的像唯一,但原像不一定唯一; (3) 映射又称为算子,在不同数学分支中有不同的名称 非空集X 数集Y 非空集X X上的变换 非空集X 实数集X X上的函数 实数集Y f X上的泛函 X Y

逆映射 >满射、单射和双射 设f是从集合X到集合Y的映射
逆映射 设f是从集合X到集合Y的映射 满射、单射和双射 X Y f

逆映射 >满射、单射和双射 设f是从集合X到集合Y的映射 ●若R,=Y,即Y中的任一元素y都是X中某元素的像, 则称f为到Y上的映射或满射 ●若对X中任意两个不同的元素X,≠x,它们的像 f(x)≠f(x,),则称f为X到Y的单射 Y=f(X)
逆映射 设f是从集合X到集合Y的映射 满射、单射和双射 若 即Y中的任一元素y都是X中某元素的像, 则称f为X到Y上的映射或满射 若对X中任意两个不同的元素 它们的像 则称f为X到Y的单射 X Y f Y=f (X)