
第五节 第三章 画数的极值与 最大值最小小值 一、函数的极值及其求法 二、最大值与最小值问题
二、最大值与最小值问题 一、函数的极值及其求法 第五节 函数的极值与 最大值最小值 第三章

一、函数的极值及其求法 定义:设函数f(x)在(a,b)内有定义,x☐(a,b) 若存在x。的一个邻域,在其中当x口xo时, (1)f(x)口f(x),则称o为f(x)的极大值点, 称f(xo)为函数的极大值; (2)f(x)口f(x),则称xo为f(x)的极小值点, 称f(x)为函数的极小值 极大值点与极小值点统称为极值点
定义: 在其中当 时, (1) 则称 为 的极大值点 , 称 为函数的极大值 ; (2) 则称 为 的极小值点 , 称 为函数的极小值 . 极大值点与极小值点统称为极值点 . 一、函数的极值及其求法
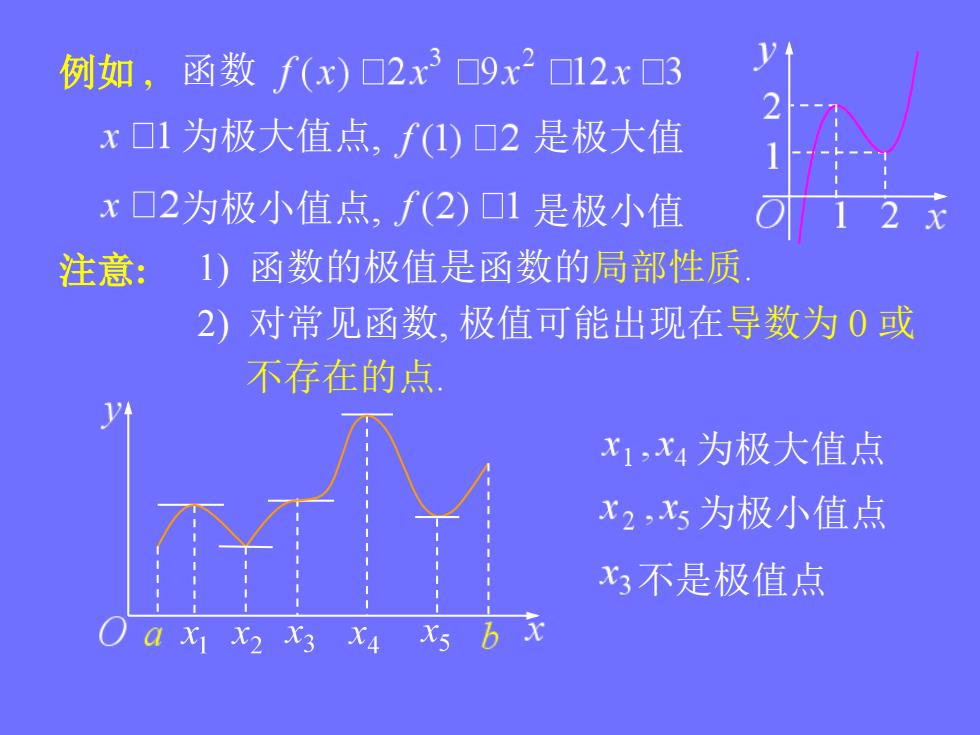
例如,函数f(x)☐2x3口9x2☐12x☐3 x口1为极大值点,f1)口2是极大值 x口2为极小值点,f(2)口1是极小值 12 注意: 1)函数的极值是函数的局部性质 2)对常见函数,极值可能出现在导数为0或 不存在的点 x1,x4为极大值点 x2,x5为极小值点 x3不是极值点 a X1 X2 X3 X4
注意: 为极大值点 为极小值点 不是极值点 2) 对常见函数, 极值可能出现在导数为 0 或 不存在的点. 1) 函数的极值是函数的局部性质. 例如 , 为极大值点, 是极大值 为极小值点, 是极小值 函数
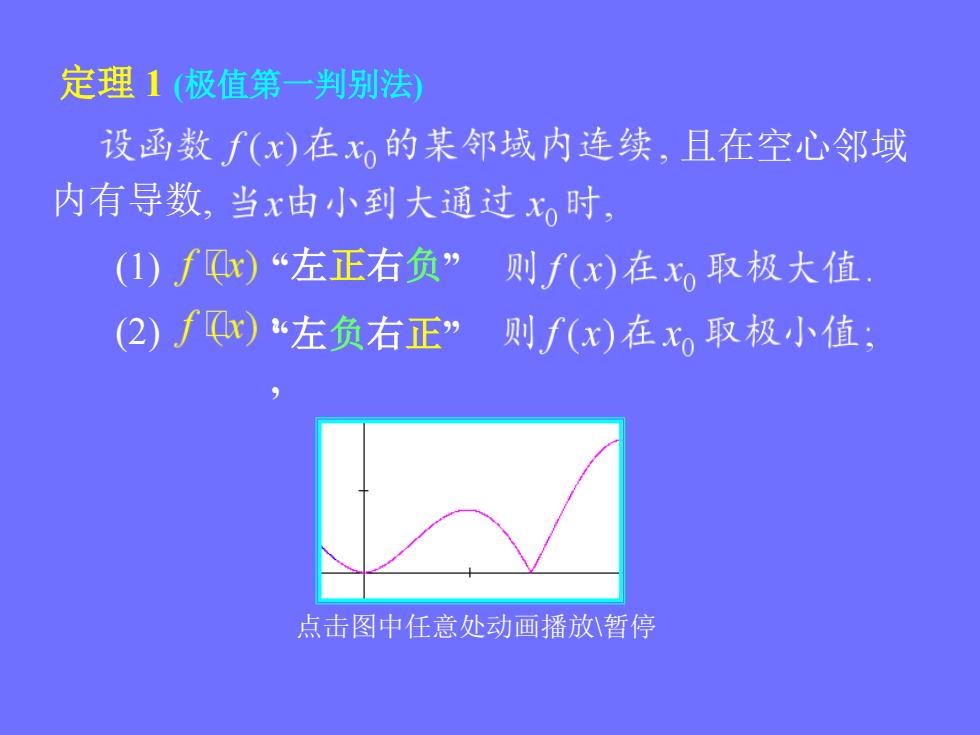
定理1(极值第一判别法 设函数f(x)在x。的某邻域内连续,且在空心邻域 内有导数,当x由小到大通过x时, (1)∫Cx)“左正右负”则f(x)在x。取极大值 (2)fx)“左负右正”则f(x)在x。取极小值 点击图中任意处动画播放暂停
定理 1 (极值第一判别法) 且在空心邻域 内有导数, (1) “左正右负” , (2) “左负右正” , 点击图中任意处动画播放\暂停

例1.求函数f(x)口(x□I)x3的极值 解:)求号数f)c(x)峰暖 2)求极值可疑点 令f0)☐0,得口2:令fx)□口,得x2□0 3)列表判别 (,0) 0.3是层,口) f( 0 f(x ☐0.33 口x口0是极大值点,其极大值为f(O)口0 x□二是极小值点,其极小值为f()口D.33
例1. 求函数 的极值 . 解: 1) 求导数 2) 求极值可疑点 令 得 令 得 3) 列表判别 是极大值点,其极大值为 是极小值点,其极小值为