
列等式: a=bq+n,0<n<b, b=n9+n,0<n<n, . (1) .2=n.14+n,0<n<n.1, a.1=qa+1+n+1,n+1=0 因为每进行一次带余数除法,余数就至少减一,而b是有限的,所 以我们最多进行b次带余数除法,总可以得到一个余数是零的等 式,即+1=0(1)式所指出的计算方法,叫作辗转相除法在西方 常把它叫做欧几里得除法,它也就是我国著名的古代数学著作《九 章算术》中提出的“更相减损术”现在我们证明 定理4若a,b是任意两个整数,则(a,b)就是(1)中最后一 个不等于零的余数,即(a,b)=rn 证由定理2,3即得 ra=(0,ra)=(ra+1,ra)) =(ra,n.1)=. =(n,b)=(a,b) 证完 由于,能够用辗转相除法直接算出,所以辗转相除法给出了求两 整数的最大公因数的实际可行的算法 由定理2,3及(1)我们还可以得到 推论4.1a,b的公因数与(a,b)的因数相同(证明留给读 者) 由以上的讨论,我们可以看到,若a,b两整数中有一为零,而 另一数不为零时,则(a,b)为不等于零的数的绝对值,若a,b两 数都不是零时,则a,b最大公因数可以由(1)实际地算出来 我们看两个例子: 例1a=-1859,b=1573,由定理1,(-1859,1573)= ·6·
列等式: a = bq1 + r1 , 0 < r1 < b, b = r1 q2 + r2 ,0 < r2 < r1 , . rn - 2 = rn - 1 qn + rn , 0 < rn < rn - 1 , rn - 1 = rn qn + 1 + rn + 1 , rn + 1 = 0 . ( 1) 因为每进行一次带余数除法,余数就至少减一, 而 b 是有限的, 所 以我们最多进行 b 次带余数除法, 总可以得到一个余数是零的等 式,即 rn + 1 = 0 .( 1) 式所指出的计算方法,叫作辗转相除法 .在西方 常把它叫做欧几里得除法 .它也就是我国著名的古代数学著作《九 章算术》中提出的“更相减损术”.现在我们证明 定理 4 若 a, b 是任意两个整数, 则( a, b) 就是 ( 1) 中最后一 个不等于零的余数,即( a, b) = rn . 证 由定理 2, 3 即得 rn = ( 0, rn ) = ( rn + 1 , rn ) = ( rn , rn - 1 ) = . = ( r1 , b) = ( a, b) . 证完 由于 rn 能够用辗转相除法直接算出, 所以辗转相除法给出了求两 整数的最大公因数的实际可行的算法 . 由定理 2, 3 及(1 )我们还可以得到 推论 4.1 a, b 的公因数与 ( a, b) 的因数相同 ( 证明留给读 者) . 由以上的讨论,我们可以看到, 若 a, b 两整数中有一为零, 而 另一数不为零时,则 ( a, b ) 为不等于零的数的绝对值, 若 a, b 两 数都不是零时,则 a, b 最大公因数可以由(1 )实际地算出来 . 我们看两个例子: 例 1 a = - 1859, b = 1573, 由定 理 1, ( - 1859, 1573 ) = · 6 ·
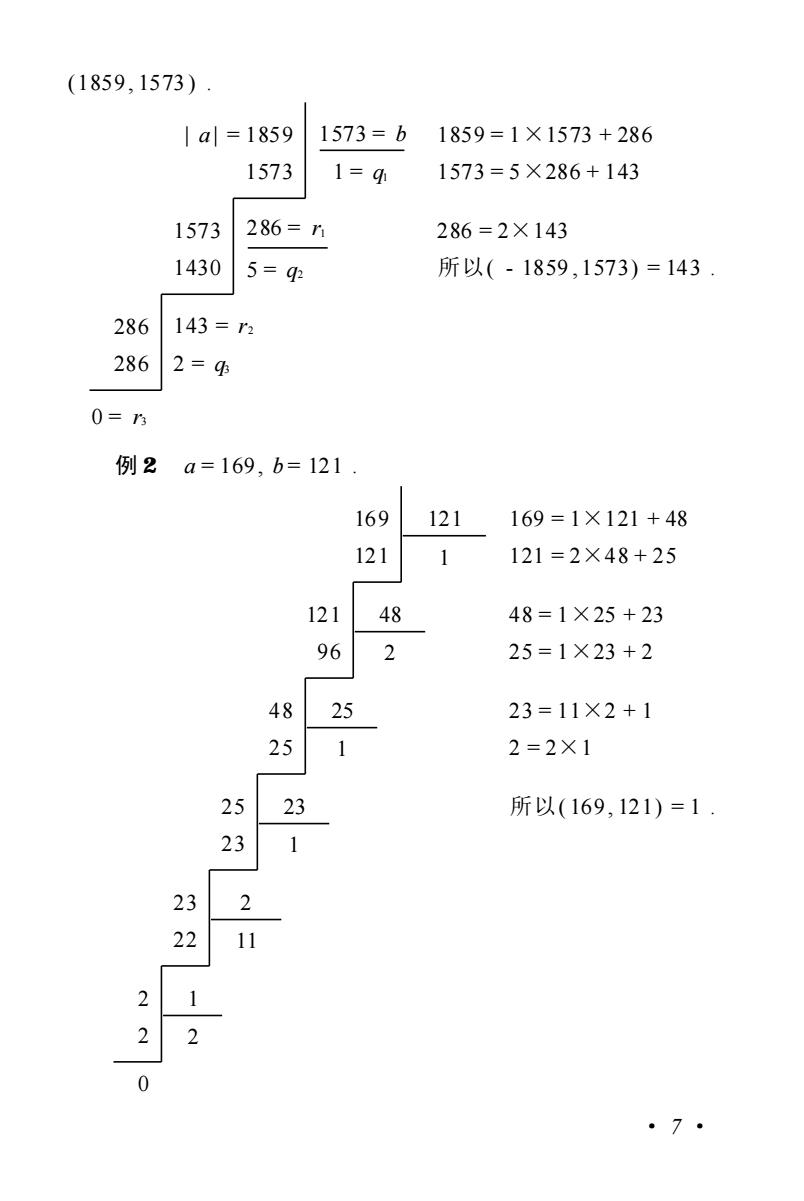
(1859,1573) 1a=1859 1573=b1859=1×1573+286 1573 1=q4 1573=5×286+143 1573 286=n 286=2×143 1430 5=q 所以(-1859,1573)=143 286143= 2862=4 0=乃 例2a=169,b=121 169 121 169=1×121+48 121 1 121=2×48+25 121 48 48=1×25+23 % 2 25=1×23+2 4825 23=11×2+1 1 2=2×1 23 所以(169,121)=1 1 32 11 1 0 ·7·
(1859, 1573 ) . | a | = 1859 { 1573 1573 = b 1 = q1 1859 = 1×1573 + 286 1573 = 5×286 + 143 1573 7 1430 286 = r1 I 5 = q2 286 = 2×143 所以( - 1859 ,1573) = 143 . 286 286 143 = r2 2 = q3 0 = r3 # 例 2 a = 169, b = 121 . 169 + 121 121 s 1 169 = 1×121 + 48 121 = 2×48 + 25 121 S 96 48 e 2 48 = 1×25 + 23 25 = 1×23 + 2 48 { 25 25 1 23 = 11×2 + 1 2 = 2×1 25 23 23 1 所以( 169, 121) = 1 . 23 22 2 11 2 2 1 2 0 · 7 ·

我们再证明两个最大公因数的性质,即 定理5设a,b是任意两个不全为零的整数,(i)若m是任 一正整数,则 (am,bm)=(a,b)m 国若6是a6的任一公因数,则号号-P,特别 h (a,b'(a,b)=1 证当a,b有一为零时,定理显然成立,今设a,b都不为零 ()由定理1,(am,bm)=(|am,|b1m),(a,b)m=(Ia, |b1)m.因此不妨假定a,b都是正数在(1)里,把各式两边同乘 以m,即得 am bm)q+rm,0<r m<bm, bm=(片m)+nm,0<5m<片m, . ra-1m=(ram)qa+1 由定理4得(am,bm)=nm=(a,b)m,因而(i)获证. (i)由(i)及定理1, 号号1=1,11=01.1=(a,. 号名-0 δ a h 当8=(a,)时,上式即为(a6(a6=1. 证完 现在来研究两个以上整数的最大公因数由定理1及2我们 不妨假设a,a,.,a.是任意n个正整数令 (a1,)=d,(d,a)=d,.,(dn.1,a)=dn.(2) 于是我们有 定理6若a1,.,an是n个整数,则(a,a,.,an)= d. ·8·
我们再证明两个最大公因数的性质,即 定理 5 设 a, b 是任意两个不全为零的整数, (i) 若 m 是任 一正整数,则 ( am , bm) = ( a, b) m . (ii) 若 δ是 a, b 的任 一公因数, 则 a δ , b δ = ( a, b) |δ| , 特 别 a ( a, b) , b ( a, b) = 1 . 证 当 a, b 有一为零时, 定理显然成立,今设 a, b 都不为零 . (i) 由定理 1, ( am , bm) = ( | a | m , | b | m ) , ( a, b) m = ( | a | , | b | ) m .因此不妨假定 a, b 都是正数 .在 ( 1 )里, 把各式两边同乘 以 m , 即得 am = ( bm ) q1 + r1 m , 0 < r1 m < bm , bm = ( r1 m) q2 + r2 m , 0 < r2 m < r1 m , . rn - 1 m = ( rn m) qn + 1 . 由定理 4 得( am , bm ) = rn m = ( a, b) m ,因而 (i)获证 . (ii) 由(i)及定理 1 , a δ , b δ |δ| = | a | |δ| |δ| , | b | |δ| |δ| = ( | a | , | b | ) = ( a, b) , 故 a δ , b δ = ( a, b) |δ| . 当 δ= ( a, b) 时,上式即为 a ( a, b) , b ( a, b) = 1 . 证完 现在来研究两个以上整数的最大公因数 .由定理 1 及 2 我们 不妨假设 a1 , a2 ,., an 是任意 n 个正整数 .令 ( a1 , a2 ) = d2 , ( d2 , a3 ) = d3 ,., ( dn - 1 , an ) = dn . ( 2) 于是我们有 定理 6 若 a1 , a2 , ., an 是 n 个整数, 则 ( a1 , a2 , ., an ) = dn . · 8 ·

证由(2),d|an,dn|dn1.但dn1|a1,dn.1|da2,故 da.,dd.2由此类推,最后得到d|a,d|a1,., dn|a,即dn是a,.,a的一个公因数又设d是a,., a的任一公因数,则da,d小&,由推论4.1,d川d,同样由推论 4.1,d川d,由此类推,最后得d|dn因而d≤|d|≤d故dn是 a,.,an的最大公因数 证完 习题 1.证明推论4.1 2.应用§1习题3证明(a,b)=ax+b,其中axo+b%是形如ax+ y(x,y是任意整数)的整数里的最小正数,并将此结果推广到n个整数的 情形 3.应用§1习题4证明任意两整数的最大公因数存在,并说明其求法 试用你所说的求法及辗转相除法实际算出(76501,9719) ·4.证明本节()式中的≤竖 §3整除的进一步性质及最小公倍数 在上节中我们看到了辗转相除法在研究最大公因数的过程中 的重要性在这一节里我们要研究上节(1)式中与a、b的关系, 由此可以得出关于整除的进一步性质此外,在本节里面还要讨论 到最小公倍数及其重要的性质 由上节,设a、b是任意两个正整数,则可以得到下列诸等式: a=bg+n,0<n<b, b=n92+n,0<n<n 中年00000 (1) -1=作g+1+m+1,0<+1<作, 00000 n.1=mqm+1. ·9
证 由 ( 2 ) , dn | an , dn | dn - 1 .但 dn - 1 | an - 1 , dn - 1 | dn - 2 , 故 dn | an - 1 , dn | dn - 2 .由 此 类 推, 最 后 得 到 dn | an , dn | an - 1 , ., dn | a1 ,即 dn 是 a1 , a2 ,., an 的一个公因数 .又设 d 是 a1 , a2 , ., an 的任一公因数, 则 d | a1 , d | a2 , 由推论 4.1, d | d2 , 同样由推论 4.1, d | d3 ,由此类推, 最后得 d | dn .因而 d≤ | d | ≤ dn .故 dn 是 a1 , a2 , ., an 的最大公因数 . 证完 习 题 1. 证明推论 4.1 . 2. 应用§1 习题 3 证明 ( a, b) = ax0 + by0 , 其中 ax0 + by0 是形如 ax + by ( x , y 是任意整数 )的整数里的最小正数 ,并将此结果推广到 n 个整数的 情形 . 3. 应用§1 习题 4 证明任意两整数的最大公因数存在 , 并说明其求法 . 试用你所说的求法及辗转相除法实际算出 (76501 ,9719) . * 4. 证明本节 (1) 式中的 n≤ 2log b log2 . §3 整除的进一步性质及最小公倍数 在上节中我们看到了辗转相除法在研究最大公因数的过程中 的重要性 .在这一节里我们要研究上节( 1) 式中 rk 与 a、b 的关系, 由此可以得出关于整除的进一步性质 .此外, 在本节里面还要讨论 到最小公倍数及其重要的性质 . 由上节,设 a、b 是任意两个正整数,则可以得到下列诸等式: a = bq1 + r1 , 0 < r1 < b, b = r1 q2 + r2 ,0 < r2 < r1 , . rk - 1 = rk qk + 1 + rk + 1 , 0 < rk + 1 < rk , . rn - 1 = rn qn + 1 . ( 1) · 9 ·

于是我们有 定理1若a,b是任意两个正整数,则 Qa-Pb=(-1)n,k=1,.,n (2) 其中 Po=1,P1=q,P=quPi.+Px.2, k=2,.,n.(3) Q=0,Q1=1,Q=kQk1+Q2, 证当k=1时,(2)显然成立,当k=2时 h=-[a4-b(1+9)] 但 1+4=P+P,4=41+0=4Q+Q, Q:a-p:b=(-1)'n,P:=g P:+P,:= 假定(2),(3)对于不超过k≥2的正整数都成立,则 (-1)n+1=(-1)(n.1-gk+1) =(Q1a-P-1b)+4k+1(2a-Pb) =(q+1O+Q.i)a-(+1P+P.1)b 故 Q+1a-P+1b=(-1)*n+1, 其中 P+1=4+1Pk+P.1,Q+1=qk+1Q+Qk.1 由归纳法,定理为真 证完 推论11若a,b是任意两个不全为零的整数,则存在两个 整数3,1使得 as+bt=(a,b) (4) 定理2若a,b,c是三个整数,且(a,c)=1,则 (i)ab,c与b,c有相同的公因数, (ii) (ab,c)=(b,c), (5) 上面假定了b,c至少有一不为零 证()由题设及推论11,存在两个整数s、t满足等式 as+ct=1. 两边乘以b,即得 (ab)s+c(bt)=b. ·10·
于是我们有 定理 1 若 a, b 是任意两个正整数, 则 Qk a - Pk b = ( - 1) k - 1 rk , k = 1,., n ; ( 2) 其中 P0 = 1 , P1 = q1 , Pk = qkPk - 1 + Pk - 2 , Q0 = 0, Q1 = 1 , Qk = qk Qk - 1 + Qk - 2 , k = 2 ,., n . ( 3) 证 当 k = 1 时, (2 )显然成立, 当 k = 2 时, r2 = - [ aq2 - b( 1 + q1 q2 ) ] . 但 1 + q1 q2 = q2 P1 + P0 , q2 = q2·1 + 0 = q2 Q1 + Q0 , 故 Q2 a - P2 b = ( - 1) 2 - 1 r2 , P2 = q2 P1 + P0 , Q2 = q2 Q1 + Q0 . 假定(2 ) , (3 )对于不超过 k≥2 的正整数都成立,则 ( - 1 ) k rk+ 1 = ( - 1 ) k ( rk - 1 - qk + 1 rk ) = ( Qk - 1 a - Pk - 1 b) + qk + 1 ( Qk a - Pk b) = ( qk+ 1 Qk + Qk - 1 ) a - ( qk + 1 Pk + Pk - 1 ) b . 故 Qk + 1 a - Pk + 1 b = ( - 1) k rk + 1 , 其中 Pk + 1 = qk + 1 Pk + Pk - 1 , Qk + 1 = qk + 1 Qk + Qk - 1 . 由归纳法,定理为真 . 证完 推论 1 .1 若 a, b 是任意两个不全为零的整数, 则存在两个 整数 s, t 使得 as + bt = ( a, b) . ( 4) 定理 2 若 a, b, c 是三个整数,且 ( a, c) = 1 ,则 (i) ab, c 与 b, c 有相同的公因数, (ii) ( ab, c) = ( b, c) , ( 5) 上面假定了 b, c 至少有一不为零 . 证 (i) 由题设及推论 1 .1,存在两个整数 s、t 满足等式 as + ct = 1 . 两边乘以 b,即得 ( ab) s + c( bt) = b . · 10 ·