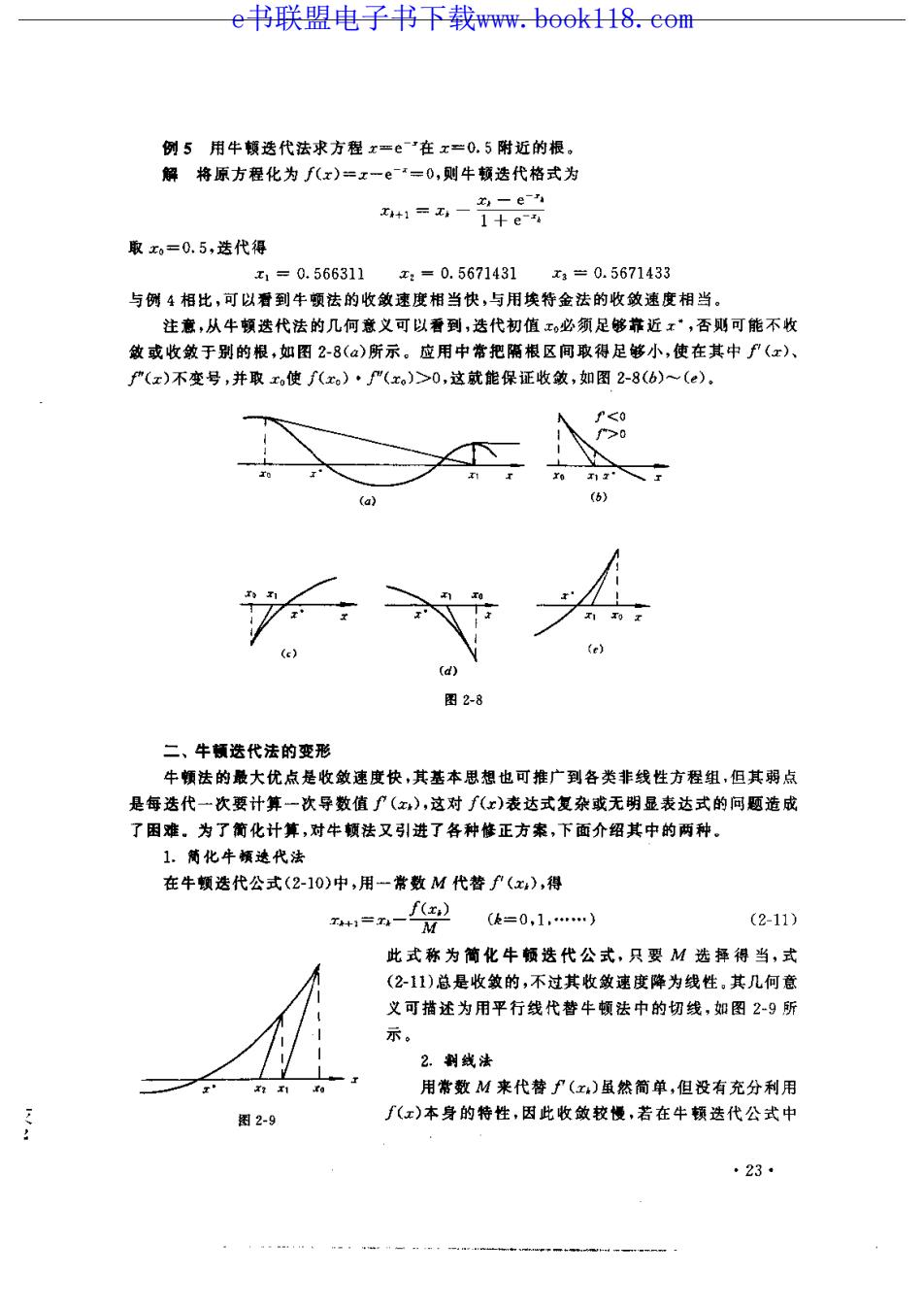
e书联盟电子书下载ww.bo6k118.e6m 例5用牛顿选代法求方程x=e在x=0.5附近的根。 解将原方程化为f(x)=x一e=0,则牛顿选代格式为 +1=无4- x,-e- 1十e-4 取=0.5,选代得 x1=0.566311 :=0.5671431 x=0.5671433 与例4相比,可以看到牛顿法的收敛速度相当快,与用埃特金法的收敛速度相当。 注意,从牛顿选代法的几何意义可以看到,选代初值必须足够靠近x',否则可能不收 或收敛于别的根,如图2-8()所示。应用中常把隔根区间取得足够小,使在其中P(x) f产(x)不变号,并取x,使f(x)·(xo)>0,这就能保证收敛,如图2-8(6)~(), (a 6》 图2-8 二、牛领选代法的变形 牛领法的最大优点是收敛速度快,其基本思想也可推广到各类非线性方程组,但其弱点 是每选代一次要计算一次导数值了(x),这对f(x)表达式复杂或无明显表达式的问题造成 了围难。为了葡化计算,对牛顿法又引进了各种修正方案,下面介绍其中的两种。 1.葡化牛颜速代法 在牛顿选代公式(2-10)中,用一常数M代替P(x,),得 =- (k=0,1,.) (2-11) 此式称为简化牛顿选代公式,只要M选择得当,式 (211)总是收敏的,不过其收敛速度降为线性,其几何意 义可描述为用平行线代替牛顿法中的切线,如图29所 示。 2割线法 用常数M来代替子(x)虽然简单,但没有充分利用 图2-9 (x)本身的特性,因此收敛较慢,若在牛顿选代公式中 ·23
e书联盟电子书下载www.book118.com

e书联盟电子书下载www.b6ok1H8.Com 改用差商)二心代替导数r(,得选代公式 x一x-1 :=五-77-D-) (2-12) 可以证明,它的牧敛阶为力=(1一√5)≈1.618,确实比 式(2-11)收效快。由图20可见,连接曲线y=f(x)上的 两点P,(五,f()与P-(-1了(x-),所得弦线与 轴交点的横坐标即为由此式求出的x+1。因此,称之为双点 削线法。其流程图可由牛顿选代法的流程图(图2?)略加 T'J 修改得到,读者可自行画出。 有时为了使程序简单,将选代公式(2-12)中的-:改 为x。,即每步迭代时只利用一个新点,这样的迭代格式 图210 称为单点副线法,然而它的收敛速度只是线性的。 三、计算重根的牛颖运代法 若x为方程f(x)=0的m(m>1)重根,则f(x)可表为 (x)=(x一x”)4g(x) 其中g()≠0,此时用牛顿选代法求x'仍然收敛,只是收敛速度将大大减慢。事实上,因为 令=x4一x‘,则 一g-=[-学a] ■ =1-元≠0 (2-13) 可见用牛法求方程的重根仅为线性收敛 为了提高求重根的收敛速度,有两种可供选择的方法,方法之一是将求重根的问题转化 为求单根。注意到函数 Q(x)=≠0,x‘是u(x)=0之单根.因此,求f(z)=0之m重根x等价于求ur)=0之 单服x·,而对红(x)=0用牛顿迭代法求根则是平方收敛的,其迭格式为 (2-14) 上述迭代格式右端较复杂,应用起来不方便。另一种求m重根的方法是采用如下选代 格式 1-4-m 2-15) 可以证明它是求m重根x~的具平方收敛的迭代格式。 ·24·
e书联盟电子书下载www.book118.com

e书联盟电子书下载www.book118.com 问题是如何确定根的重数m?下面介绍一个边选代边估计重数的方法。设4-1 为用牛顿法代格式(2-10)所得三个相邻的选代值,令 (x,一x)一(x1一x”) 1-4- ‘1 由式(2-13)可知 m4=1-=m1 华 =二” 因此可用下式估计m m≈ (2-16) 例6用牛缬选代法求方程f(x)=(x一1)[sin(x-1)+3z]-x3+1=0在0.95附近 之根。 解取=0.95,用牛顿选代法式(210)求得的见表2-3,由表中数据可见4收敛很 便。由亡入心2可知,所求根为m一2重根,政用式(2-15)法代格式,得 ◆ 6=0.95 x1=0.9988559 ==1 收敛速度大大快于直接用牛顿选代公式(2-10)。 表2-3 0.95 0.9744279 0.987583 .993873 0.5090 2.0369 32 2.0190 0.5007 02 0.9991901 0.5123 .051 第四节解非线性方程组的牛顿法 上节采用非线性方程线性化的方法引人了方程求根的牛顿选代公式,这个线性化的方 法也可用来解决非线性方程组的求解问题,下面以两个未知量,两个方程的情况为例加以说 明· ·25
e书联盟电子书下载www.book118.com

e书联盟电子书下载www.book1H8.com 设非线性方程组为 [u(x,¥)=0 v(r,y)-0 (2-17) 已知P,(xn)是该方程组的一组近似解,要求得到更精骑的解。为此,将函数“,v在P)点 附近用一阶奏勒多项式近似表示 r,y》w)+x-+y-) 其中偏导数在P。点取值,于是,在P。附近非线性方程组(2-17)可用下述线性方程组近似代 楼 鹿-0+0y-w=-u (2-18) 由偏导数组成的矩阵 称为雅可比(acobi)矩阵,对应的行列式称为雅可比行列式。线性方程组(2-18)的系数行列 式即为雅可比行列式在P,点的值,设其满足 J= ≠0 用克莱舞(Cramer)法则可求得方程组(2-18)的解 =7, 则()即是方程组(2-1?)的新近似解.照此分析,若已知近似解(,y),设雅可比行列式 在P()点的值不为零 = ≠0 y 则求(x+1,+1)的迭代公式为 a 4 (2-19) 26
e书联盟电子书下载www.book118.com

e书联盟电子书下载www.book118.com 这就是求解非线性方程组(2-17)的牛顿达代公式。 例7用牛顿法求下述方程组在P,=()=(1,1)附近的解 1u(x,y)=T+2-5=0 (x,y)=(x+1)y一(3x+1)■0 解雅可比矩阵为 在P,(1,1)点,%=1+1-5=-3,%=2-4=-2J。=8≠0,于是 12-3 4-1-2二2=1+-2+ 再从P(,为)出发,可求出 x2=1 =2+36 此方程组的准确是工=1,y=2,可见(x2,)已有很高精度, 以上方法完全可以推广到解一般非线性方程组,因为计算量太大,对应的线性方程组不 要用克莱姆法则求解,而应采用下一章介绍的方法求解。 同方程求根的情形一样,用牛顿法解非线性方程组时,选代初值应充分靠近所求解,香 则不能保证收敛性。此外,为了避免求偏导数,也可用差商代替之。 第五节劈因子法 考惠刀次实系数代数方程 f(x)=ao+ax1十.十a=0 2-20) 由代数学可知,∫(x)=0有n个根,其中可能有实根,也可能有成对出现的共轭复根。本节介 绍一种既可求其实根,也可求其复根的方法一劈因子法。 劈因子法的基本思路是先给出 一个初始二次式 w(x)=Y十z十) (2-21) 用w(x)去除f(x),得商式Q(x)与余式R(r) Q(x)=bnr1+bx-1+.+b.-: R(x)=ror十ra 因此 」(x)=(x2十x十)Q(x)十R(x) (2-22) 当r,l、r,l均小于给定的误差限e时,则可认为(x)为fx)的近似二次因式,令u(r)=0 可得f(x)=0的两个近似根 x=2(-u士√m-4和) (2-23) .27·
e书联盟电子书下载www.book118.com