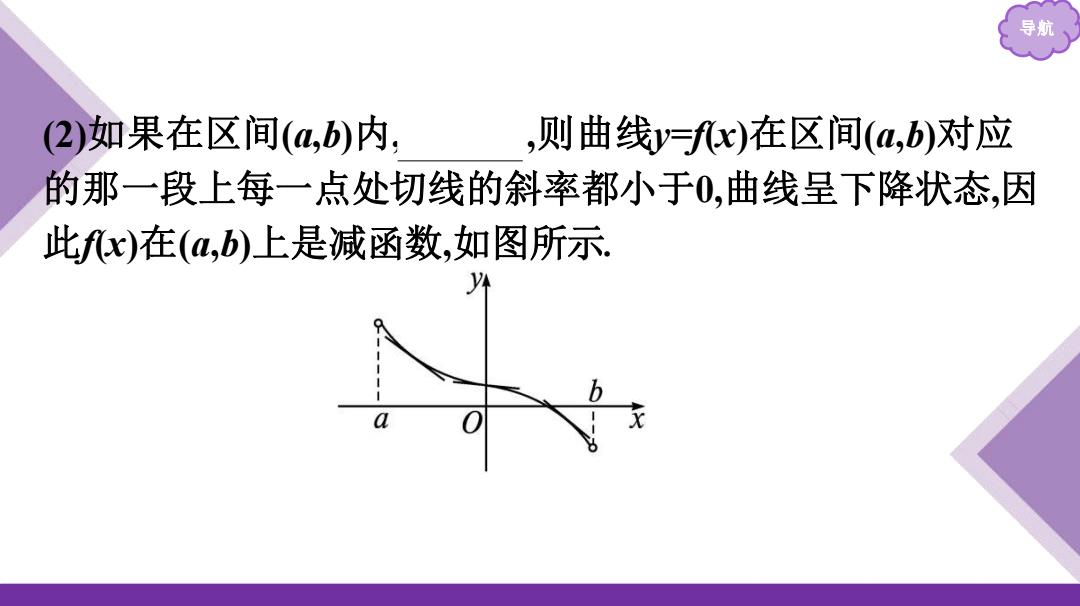
导 (2)如果在区间(4,b)内 ,则曲线y=fx)在区间(a,b)对应 的那一段上每一点处切线的斜率都小于0,曲线呈下降状态,因 此fx)在(a,b)上是减函数,如图所示
导航 (2)如果在区间(a,b)内, f'(x)<0 ,则曲线y=f(x)在区间(a,b)对应 的那一段上每一点处切线的斜率都小于0,曲线呈下降状态,因 此f(x)在(a,b)上是减函数,如图所示

3.若函数y=fx)是定义在R上的增函数,则f'x)>0是否一定成 立? 提示:不一定.如函数fx)=3在R上为增函数,但当x=0 时f(0)=0. 4.设函数y=fx)在区间(a,b)内可导. (1)若fx)在区间(4,b)内单调递增,则fx)≥0在区间(a,b)内恒成 立,且x)在区间(a,b)的任意子区间内都不恒等于0; (2)若fx)在区间(a,b)内单调递减,则fx)≤0在区间(a,b)内恒成 立,且fx)在区间(,b)的任意子区间内都不恒等于0
导航 3.若函数y=f(x)是定义在R上的增函数,则f'(x)>0是否一定成 立? 提示:不一定.如函数f(x)=x3在R上为增函数,但当x=0 时,f'(0)=0. 4.设函数y=f(x)在区间(a,b)内可导. (1)若f(x)在区间(a,b)内单调递增,则f'(x)≥0在区间(a,b)内恒成 立,且f'(x)在区间(a,b)的任意子区间内都不恒等于0; (2)若f(x)在区间(a,b)内单调递减,则f'(x)≤0在区间(a,b)内恒成 立,且f'(x)在区间(a,b)的任意子区间内都不恒等于0
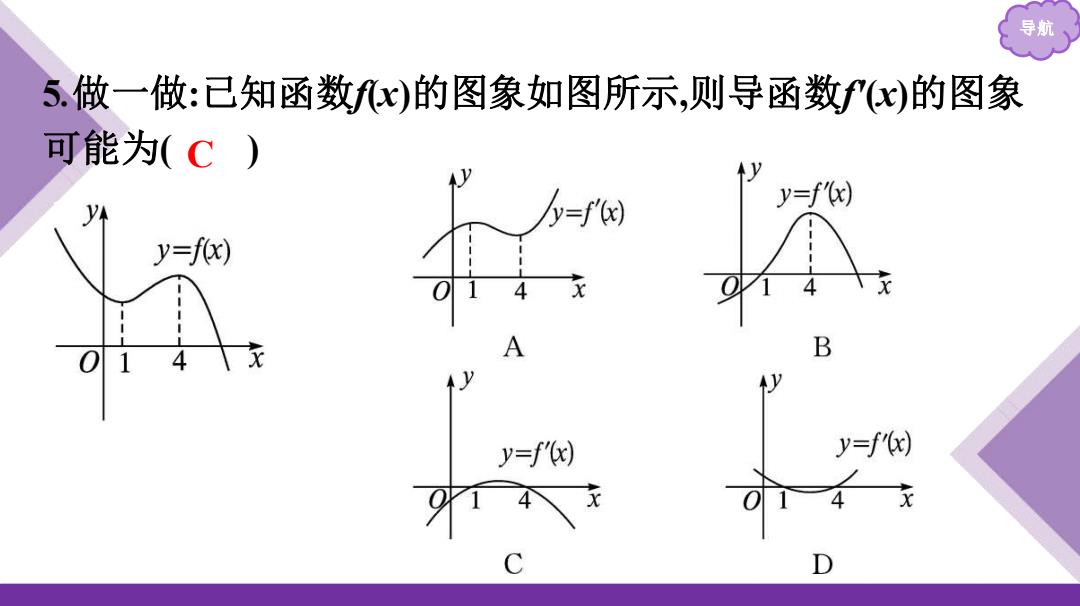
导期 5.做一做:已知函数fx)的图象如图所示,则导函数fx)的图象 可能为(C) =f') y=f'(x) y=f(x) y=f') y=f(x)
导航 5.做一做:已知函数f(x)的图象如图所示,则导函数f'(x)的图象 可能为( C )

导期 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“X”. (1)函数fx)在区间化12)内的导数比在区间心2K3)内的导数大 则函数x)在区间化1x2)内比在区间化2x3)内增长得快() (2)若fx)≥0在区间(a,b)内恒成立,则fx)在区间(4,b)内单调递 增.(:)
导航 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“×” . (1)函数f(x)在区间(x1 ,x2 )内的导数比在区间(x2 ,x3 )内的导数大, 则函数f(x)在区间(x1 ,x2 )内比在区间(x2 ,x3 )内增长得快.( × ) (2)若f(x)≥0在区间(a,b)内恒成立,则f(x)在区间(a,b)内单调递 增.( × )
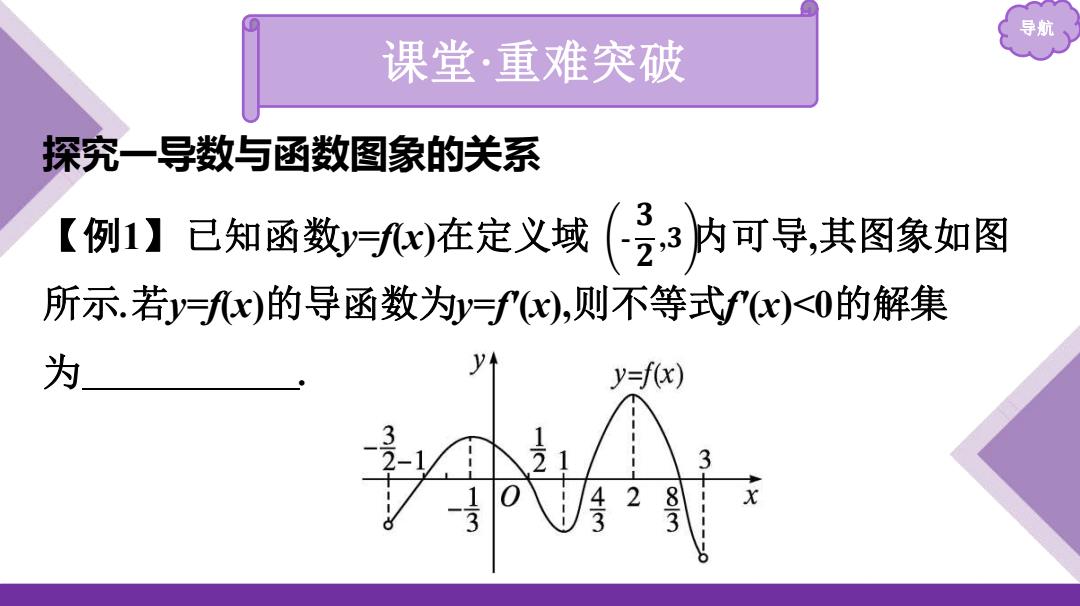
导航 课堂·重难突破 探究一导数与函数图象的关系 【例1】已知函数yfx)在定义域 (3内可导,其图象如图 所示.若y=fx)的导函数为y=fx),则不等式fx)<0的解集 为 y y=f(x) 3 2乳
导航 课堂·重难突破 探究一导数与函数图象的关系 【例1】已知函数y=f(x)在定义域 内可导,其图象如图 所示.若y=f(x)的导函数为y=f'(x),则不等式f'(x)<0的解集 为 . - 𝟑 𝟐 ,𝟑