
2.填空:(1)一般地,设函数y=fx)的定义域为D,设x∈D,如果对 于x附近的任意不同于x的x,都有 ① ,则称为函数fx)的一个极大值点,且x)在x处 取极大值; ② 则称x为函数fx)的一个极小值点,且fx)在x处 取极小值 极大值点与极小值点都称为 ,极大值与极小值都称为
导航 2.填空:(1)一般地,设函数y=f(x)的定义域为D,设x0∈D,如果对 于x0附近的任意不同于x0的x,都有 ① f(x)<f(x0 ) ,则称x0为函数f(x)的一个极大值点,且f(x)在x0处 取极大值; ② f(x)>f(x0 ) ,则称x0为函数f(x)的一个极小值点,且f(x)在x0处 取极小值. 极大值点与极小值点都称为 极值点 ,极大值与极小值都称为 极值

2)一般地,如果x是y=fx)的极值点,且fx)在x处可导,则必有 3)一般地,设函数fx)在x处可导,且fco)=0. ①如果对于x左侧附近的任意x,都有 ,对于x右侧附近 的任意x,都有 ,那么此时是fx)的极大值点. ②如果对于x左侧附近的任意x,都有 ,对于x右侧附近 的任意,都有 ,那么此时x是fx)的极小值点. ③如果fx)在x的左侧附近与右侧附近均为 (或均为 ),则x,一定不是y=fx)的极值点
导航 (2)一般地,如果x0是y=f(x)的极值点,且f(x)在x0处可导,则必有 f'(x0 )=0 . (3)一般地,设函数f(x)在x0处可导,且f'(x0 )=0. ①如果对于x0左侧附近的任意x,都有 f'(x)>0 ,对于x0右侧附近 的任意x,都有 f'(x)<0 ,那么此时x0是f(x)的极大值点. ②如果对于x0左侧附近的任意x,都有 f'(x)<0 ,对于x0右侧附近 的任意x,都有 f'(x)>0 ,那么此时x0是f(x)的极小值点. ③如果f'(x)在x0的左侧附近与右侧附近均为正号 (或均为 负号 ),则x0一定不是y=f(x)的极值点
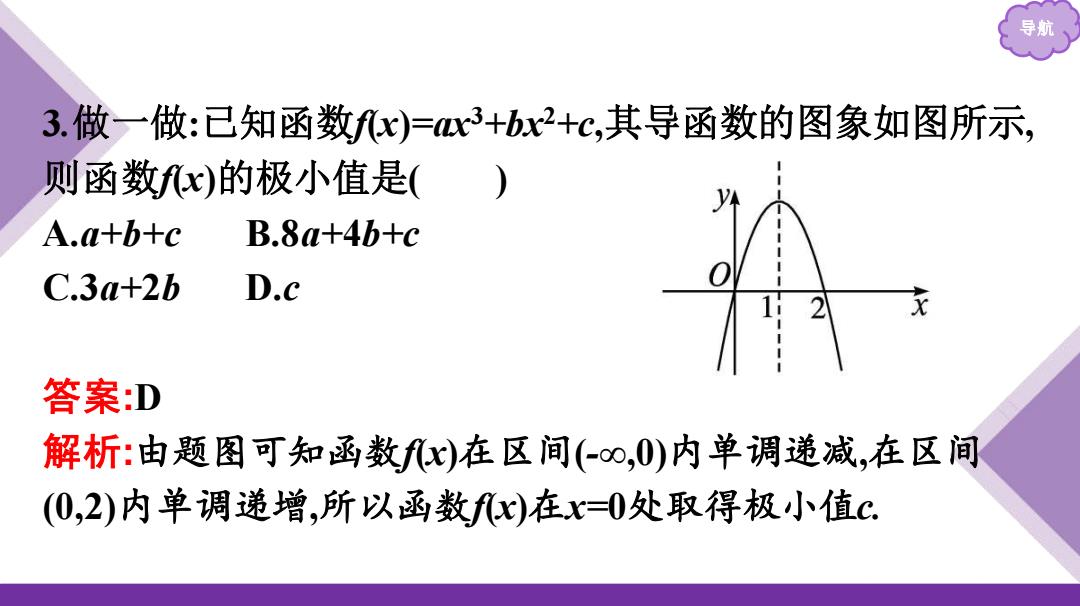
3.做一做:已知函数fx)=c3+bx2+c,其导函数的图象如图所示, 则函数fx)的极小值是( A.a+b+c B.8a+4b+c C.3a+2b D.c 2 答案:D 解析:由题图可知函数fx)在区间(-oo,0)内单调递减,在区间 (0,2)内单调递增,所以函数fx)在x=0处取得极小值c
导航 3.做一做:已知函数f(x)=ax3+bx2+c,其导函数的图象如图所示, 则函数f(x)的极小值是( ) A.a+b+c B.8a+4b+c C.3a+2b D.c 答案:D 解析:由题图可知函数f(x)在区间(-∞,0)内单调递减,在区间 (0,2)内单调递增,所以函数f(x)在x=0处取得极小值c

【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“X”. (1)函数的极大值一定大于极小值( (2)函数在某区间上或定义域内的极大值是唯一的.() (3)可导函数fx)在区间(4,b)内一定有极值.() (4)若函数fx)在区间(a,b)内有极值,则方程fx)=0在区间(,b) 内一定有解( (5)函数fx)=x3+x2+bx+c有极值的充要条件是 f'x)=3x2+2ac+b=0有解,即4≥0.()
导航 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“×” . (1)函数的极大值一定大于极小值.( × ) (2)函数在某区间上或定义域内的极大值是唯一的.( × ) (3)可导函数f(x)在区间(a,b)内一定有极值.( × ) (4)若函数f(x)在区间(a,b)内有极值,则方程f'(x)=0在区间(a,b) 内一定有解.( √ ) (5)函数f(x)=x3+ax2+bx+c有极值的充要条件是 f'(x)=3x 2+2ax+b=0有解,即Δ≥0.( × )

导航 课堂·重难突破 探究一求函数的极值 【例1】求下列函数的极值点和极值 (x)字2-3x+3: (2e)3+3nx 分析:求x)的定义域→求fx)→解方程∫x)=0→列表分析 结论
导航 课堂·重难突破 探究一求函数的极值 【例1】求下列函数的极值点和极值. (1)f(x)= 𝟏 𝟑 x 3 -x 2 -3x+3; (2)f(x)= 𝟑 𝒙 +3ln x. 分析:求f(x)的定义域→求f'(x)→解方程f'(x)=0→列表分析→ 结论