山东农业大 方本堂 二、曲面的面积 设光滑曲面S:z=f(x,y),(x,y)∈D 则面积A可看成曲面上各点M(x,y,z) 处小切平面的面积dA无限积累而成! 设它在D上的投影为do,则 doy do=cosy.d4 1+fx2(x,)+f2(x,y) dA=1+f2(x,y)+fy2(x,y)do (称为面积元素)
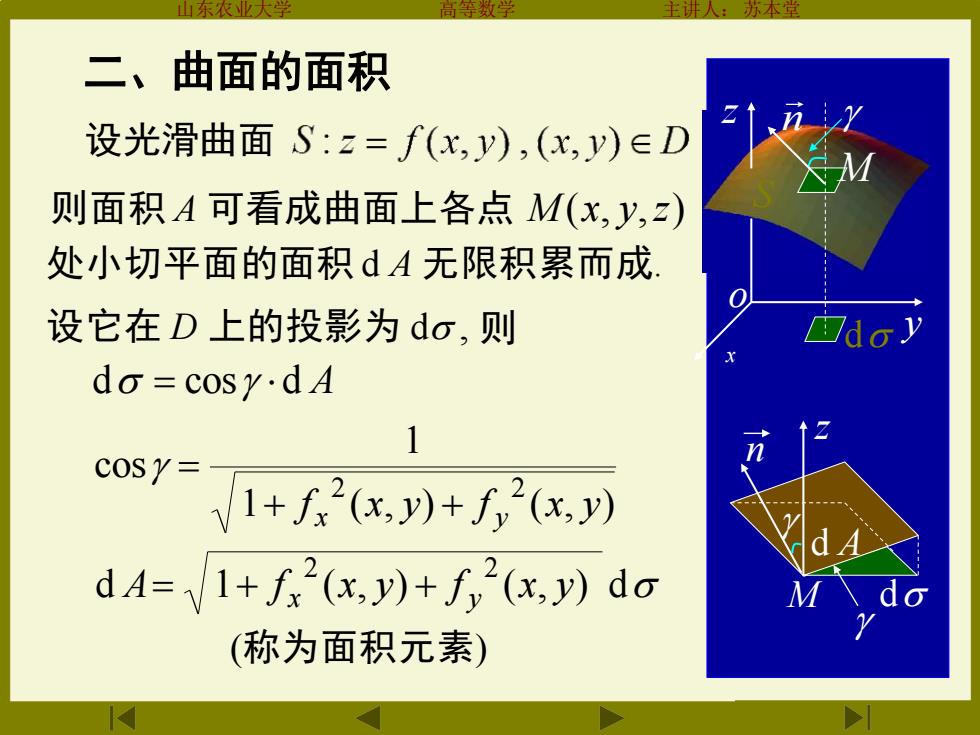
山东农业大学 高等数学 主讲人:苏本堂 M d A z d n 二、曲面的面积 x y z S o 设光滑曲面 则面积 A 可看成曲面上各点 M (x, y,z) 处小切平面的面积 d A 无限积累而成. 设它在 D 上的投影为 d , d = cos d A 1 ( , ) ( , ) 1 cos 2 2 f x y f x y + x + y = d 1 ( , ) ( , ) d 2 2 A f x y f x y = + x + y (称为面积元素) 则 M n d

故有曲面面积公式 A=1+2(x.y)+f2(x.y)da 即 4n1+2+导axdy 若光滑曲面方程为x=g(y,z),(y,)∈Dy:,则有 D 1) 若光滑曲面方程为y=h(2,x),(z,x)∈Dx,则有 4=川++dd
山东农业大学 高等数学 主讲人:苏本堂 故有曲面面积公式 1 ( , ) ( , ) d 2 2 = + + D x y A f x y f x y x y y z x z A D 1 ( ) ( ) d d 2 2 + = + 若光滑曲面方程为 ( , ) , ( , ) , Dy z x = g y z y z 则有 Dy z 即 z x x y z y A 1 ( ) ( ) d d 2 2 + = + 若光滑曲面方程为 ( , ) , ( , ) , Dz x y = h z x z x 则有

例3求半径为R的球的表面积. 解球面的面积A为上半球面面积的两倍, 球心在原点的上半球面的方程为z=√R2-x2-y2,而 -x -y OxR2-x0R2-x22 所以 12+象+ x2+y2≤R 2胶-2a rdr =-4πRVR2-r2|8=4πR2. 反常积分
山东农业大学 高等数学 主讲人:苏本堂 解 球面的面积A为上半球面面积的两倍 例3 求半径为R的球的表面积 2 2 2 R x y x x z − − − = 2 2 2 R x y y y z − − − = 2 2 2 R x y x x z − − − = 2 2 2 R x y y y z − − − = 所以 2 2 2 1 ( ) ( ) 2 2 2 y z x z A x y R + = + + dxdy R x y R x y R 2 2 2 2 2 2 2 − − = + − = 2 0 0 2 2 2 R R d R d 球心在原点的上半球面的方程为 2 2 2 z= R − x − y 而 2 0 2 2 4 R R 4 R R =− − = 2 0 0 2 2 2 R rdr R d R r = − 2 2 0 4 R = − − R R r
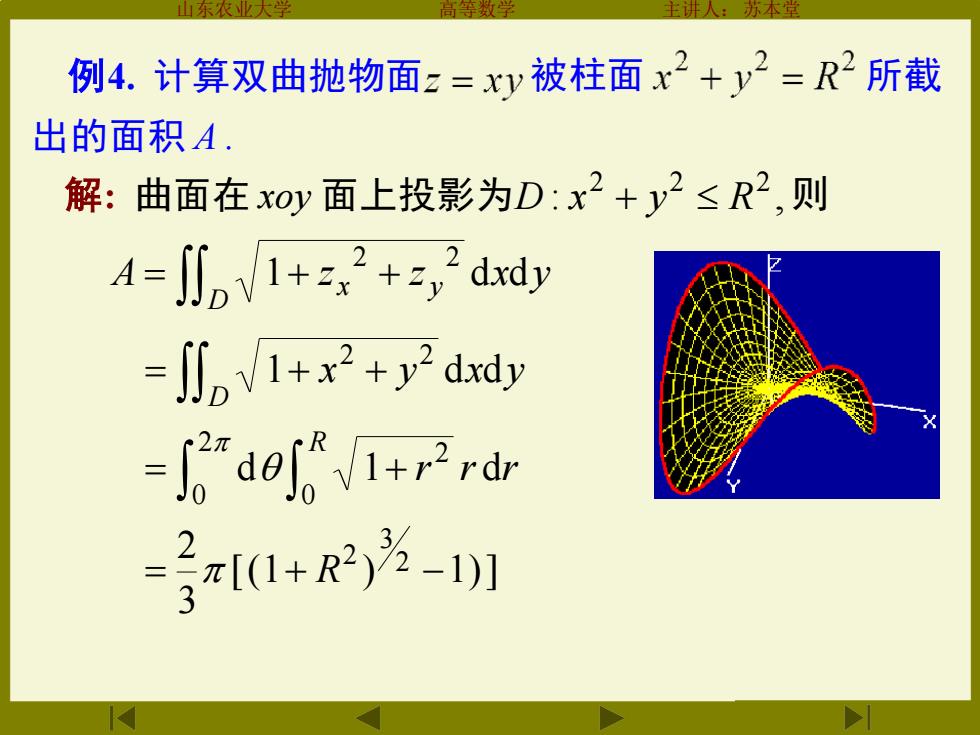
例4.计算双曲抛物面z=xy被柱面x2+y2=R2所截 出的面积A. 解:曲面在x0y面上投影为D:x2+y2≤R2,则 A=川nN1+z2+,2ddy =j川nV1+x2+y2dxd -dord 3a1+R2)为-1)1
山东农业大学 高等数学 主讲人:苏本堂 例4. 计算双曲抛物面 被柱面 所截 解: 曲面在 xoy 面上投影为 : , 2 2 2 D x + y R 则 A z z x y D x y 1 d d 2 2 = + + x y x y D 1 d d 2 2 = + + r r r R d 1 d 0 2 2 0 = + [(1 ) 1)] 3 2 2 3 2 = + R − 出的面积 A