
第八章 第二节二重积分的计算方法 (Calculation of Double Integral) 一、利用直角坐标计算二重积分 二、利用极坐标计算二重积分 三、小结与思考练习 2009年7月25日星期六 1 目录 (上页 下页 返回
2009年7月25日星期六 1 目录 上页 下页 返回 第二节 二重积分的计算方法 第八章 (Calculation of Double Integral) 一、利用直角坐标计算二重积分 二、利用极坐标计算二重积分 三、小结与思考练习
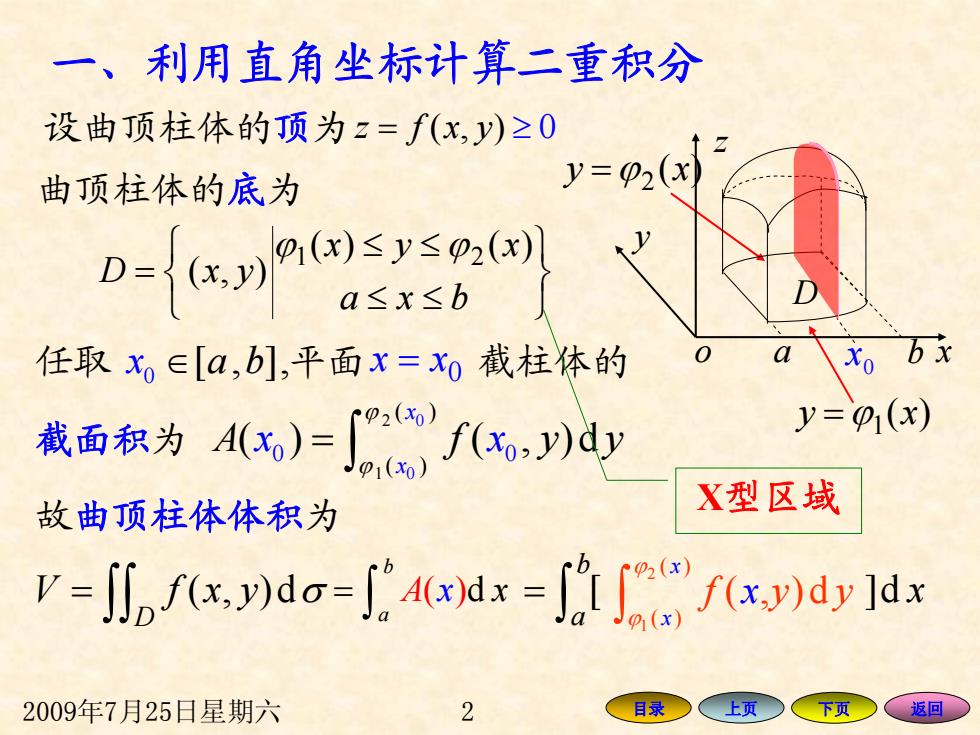
一、利用直角坐标计算二重积分 设曲顶柱体的顶为z=∫(x,y)≥0 曲顶柱体的底为 y=02(x) -ga ↑ 任取x∈[a,b],平面x=xo截柱体的 xo bx 拔西积为4x)-f化ay y=0(x) 故曲顶柱体体积为 X型区域 Vfd-x)dy ldx 2009年7月25日星期六 2 目录 上页 下页 返回
2009年7月25日星期六 2 目录 上页 下页 返回 一、利用直角坐标计算二重积分 x b a d] [ ∫ = 曲顶柱体的 底 为 ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ≤≤ ≤ ≤ = bxa xyx yxD )()( ),( ϕ1 ϕ 2 任取 0 x ∈[ , ], a b 平面 0 = xx 故曲顶柱体体积 为 ∫ ∫ = D V yxf d),( σ 0 0 2 1 ( ) ( ) 0 0 ( ) ( , )d x x A f x x y y ϕ ϕ = 截面积 为 ∫ 2 1 ( ) ( ) ( , )d x x f y x y ϕ ∫ϕ ( ) d b a = A x x ∫ 截柱体的 )( 2 y = ϕ x )( 1 y = ϕ x z x y o a b 0 x D 设曲顶柱体的 顶 为z f = ( , x y ) ≥ 0 X型区域

同样,若曲顶柱的底为 D={(x,y)41(y)≤x≤2(y),c≤y≤d} 则其体积可按如下两次积分计算 y r=∬pfxy)do f(dxdy dydx Y型区域 2009年7月25日星期六 3 目录 上页 下页 、返回
2009年7月25日星期六 3 目录 上页 下页 返回 y d c o x )( 2 x = ψ y )( 1 x = ψ y y y d c [ d] ∫ = = { ψ 1 ≤ ≤ ψ 2 ),()(),( ≤ ≤ dycyxyyxD } 同样, 若曲顶柱的底为 则其体积可按如下两次积分计算 ∫∫ = D V yxf d),( σ 2 1 ( ) ( ) ( , )d y y f x x y ψ ∫ψ 2 1 ( ) ( ) ( , )d y y f x x y ψ ∫ ∫ψ = d c d y Δ Y型区域

说明:(1)若积分区域既是X-型区域又是Y-型区域, 则有 J∬nfx,y)drdy d =axny x =Vi 2(y) =dfxr 为计算方便,可选择积分序,必要时还可以交换积分序 (2)若积分域较复杂,可将它分成若千y X型域或Y型域,则 ,=n+j,+小o 2009年7月25日星期六 目录 上页 下页 返回
2009年7月25日星期六 4 目录 上页 下页 返回 o x y ∫∫D dd),( yxyxf )( 2 为计算方便,可选择积分序, 必要时还可以交换积分序. y = ϕ x o x y D a b )( 1 x = ψ y )( 2 x = ψ y d c 则有 x )( 1 y = ϕ x y yyxf x x d),( )( )( 2 1 ∫ ϕ ∫ ϕ = b a d x xyxf y y d),( )( )( 2 1 ∫ ψ ∫ ψ = d c d y (2) 若积分域较复杂,可将它分成若干 D 1 D 2 D 3 X-型域或 Y-型域 , ∫∫∫∫ ∫ ∫ ∫ ∫ ++= 1 2 DDDD 3 则 说明 : (1) 若积分区域既是X–型区域又是 Y –型区域

补充说明(课本没有): 当被积函数∫(x,y)在D上变号时,由于 fx)=fx月+f)_x,yy-f,) 2 2 f(x,y) f2(x,y)均非负 .∬nfx,y)dxdy=∬nfx,y)dxdy -J∬n(x,)dxdy 因此上面讨论的累次积分法仍然有效. 2009年7月25日星期六 5 目录 上页 下页 返回
2009年7月25日星期六 5 目录 上页 下页 返回 f x y),( − + = 2 ),(),( ),( f yx f yx yxf 2 f yx − f yx ),(),( ),( 1f x y ),( 2f x y 均非负 ∫ ∫ ∫ ∫ ∴ = D D dd),(dd),( yxyxfyxyxf 1 在 D 上变号 时, 由于 因此上面讨论的累次积分法仍然有效 . ∫∫ − D dd),( yxyxf2 当被积函数 补充说明(课本没有):