
新课引入 在前面研究过的积分中,重积分和曲线积分都可转化 为定积分来计算,因此,我们可猜想: 曲线积分也可转化为重积分来计算 这个猜想是正确的.本节将要介绍的格林公式给出了 平面闭区域D上的二重积分与其边界曲线L上的曲线积 分之间的联系. 另一方面,我们可以利用格林公式得到“平面上积分 与路径无关的条件”和“二元函数的全微分求积的充要 条件”。 2009年7月27日星期一 目录 上页 下页 返回
2009年7月27日星期一 1 目录 上页 下页 返回 新课引入 在前面研究过的积分中,重积分和曲线积分都可转 化 为定积分来计算,因此,我们可猜想: 曲线积分也可转化为重积分来计算. 这个猜想是正确的. 本节将要介绍的格林公式给出 了 平面闭区域 D 上的二重积分与其边界曲线 L 上的曲线积 分之间的联系 . 另一方面,我们可以利用格林公式得到“平面上积分 与路径无关的条件”和“ 二 元函数的全微分求积的充要 条件”

第九章 第三节格林公式 Green Formula) 一、格林公式 二、平面上曲线积分与积分路径无关的条件 三、二元函数的全微分求积 四、小结与思考练习 2009年7月27日星期一 2 目录 上页 下页 、返回
2009年7月27日星期一 2 目录 上页 下页 返回 第三节 格林公式 第九章 (Green Formula) 一、格林公式 二、平面上曲线积分与积分路径无关的条件 三、二元函数的全微分求积 四、小结与思考练习
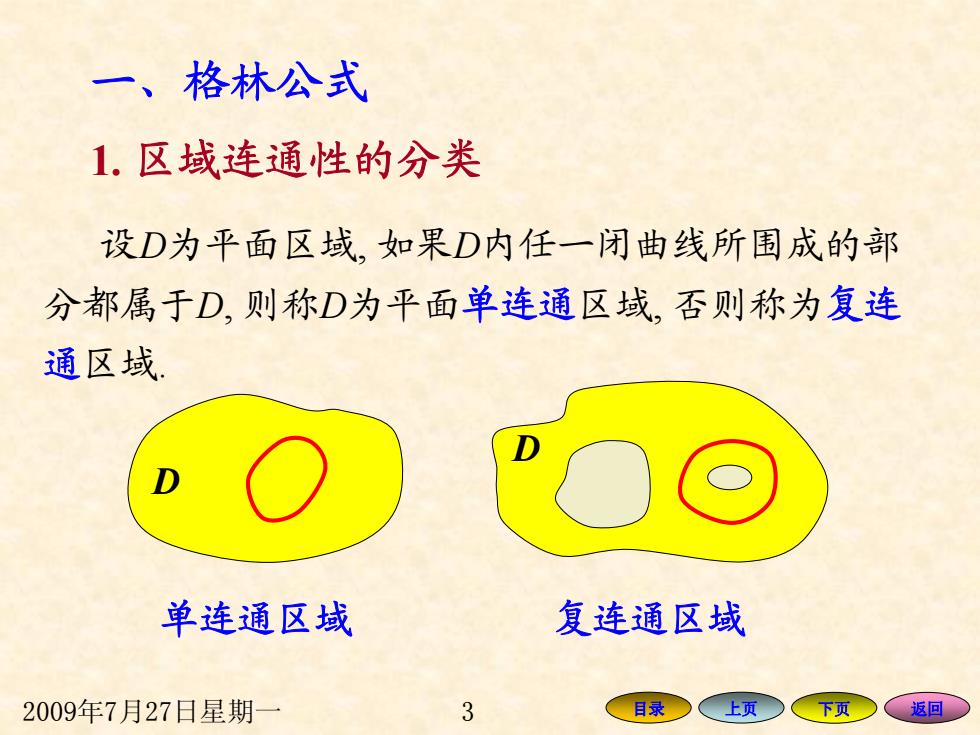
一、格林公式 1.区域连通性的分类 设D为平面区域,如果D内任一闭曲线所围成的部 分都属于D,则称D为平面单连通区域,否则称为复连 通区域」 单连通区域 复连通区域 2009年7月27日星期一 3 目录 上页 下页 返回
2009年7月27日星期一 3 目录 上页 下页 返回 一、格林公式 1. 区域连通性的分类 设D为平面区域, 如果 D内任一闭曲线所围成的部 分都属于 D, 则称 D为平面单连通区域, 否则称为复连 通区域. 单连通区域 复连通区域 D D

2、格林公式 定理1闭区域D由分段光滑的曲线L围成,函 数P(x,y)及Q(x,y)在D上具有一阶连续偏导数, 则有 叮-d-f版+Q (1) 其中L是D的取正向的边界曲线。 公式(1)叫做格林公式 2009年7月27日星期一 4 目录 上页 下页 、返回
2009年7月27日星期一 4 目录 上页 下页 返回 定理 1 闭区域 D由分段光滑的曲线 L围成,函 数 P x y 及 Q x y),(),( 在 D上具有一阶连续偏导数, 则有 ∫∫ ∫ += ∂ ∂ − ∂ ∂ L D dxdy QdyPdx y P x Q )( (1) 其中 L 是 D的取正向的边界曲线。 公式(1)叫做格林公式. 2、格林公式
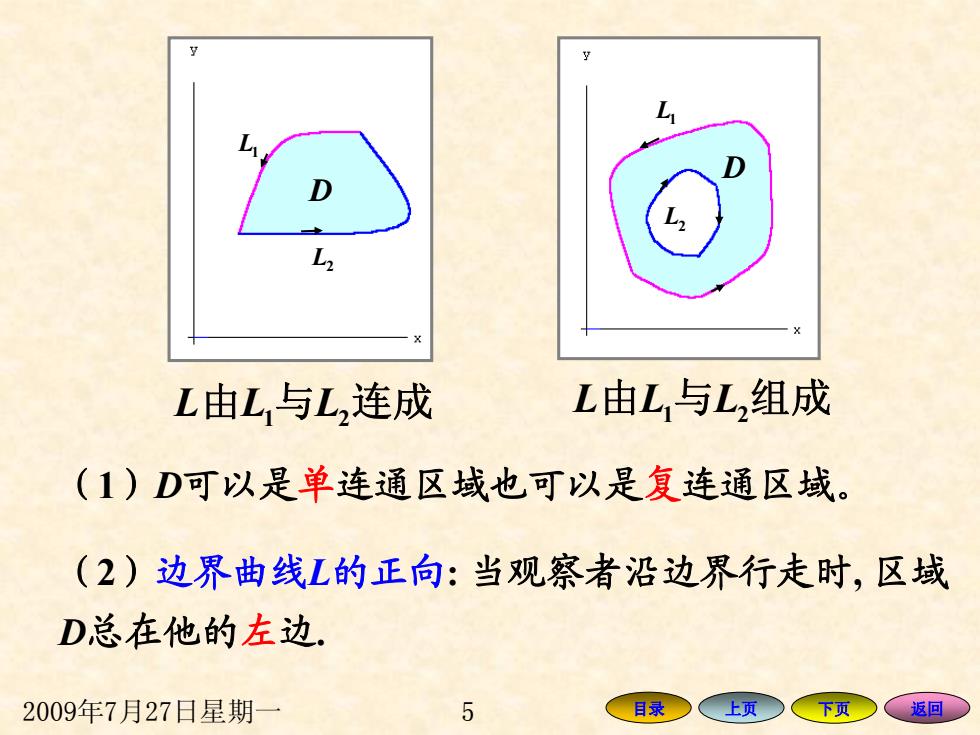
L由L,与L,连成 L由L与L,组成 (1)D可以是单连通区域也可以是复连通区域。 (2)边界曲线L的正向:当观察者沿边界行走时,区域 D总在他的左边. 2009年7月27日星期一 5 目录 上页 下页 返回
2009年7月27日星期一 5 目录 上页 下页 返回 与由 LLL 21 连成 ( 1 ) D可以是 单连通区域也可以是 复连通区域。 L 2 D L1 与由 LLL 21 组成 L 2 L1 D ( 2 )边界曲线 L的正向: 当观察者沿边界行走时, 区域 D总在他的 左 边