
新课引入 格林公式表达了平面区域上二重积分与其边界曲 线上的曲线积分之间的关系。而在空间上,也有同样 类似的结论,这就是高斯公式,它表达了空间区域上 三重积分与区域边界曲面上曲面积分之间的关系。 斯托克斯公式是格林公式的推广.后者表达了平 面闭区域二重积分与其边界曲线上的曲线积分之间的 关系,而前者则表达了曲面积分与曲面边界曲线的曲 线积分之间的联系. 这节课我们就来学习高斯公式和斯托克斯公式! 2009年7月27日星期一 目录 上页 下页 返回
2009年7月27日星期一 1 目录 上页 下页 返回 新课引入 格林公式 表达了平面区域上二重积分与其边界曲 线上的曲线积分之间的关系。而在空间上, 也有同样 类似的结论,这就是高斯公式,它表达了空间区域上 三重积分与区域边界曲面上曲面积分之间的关系。 斯托克斯公式 是格林公式的推广.后者表达了平 面 闭 区 域二重积分与 其 边界曲线上的曲线积分之间的 关系,而前者则表达了曲面积分与曲面边界曲线的曲 线积分之间的联系. 这节课我们就来学习高斯公式 和斯托克斯公式!

第九章 第六节高斯公式斯托克斯公式 Gauss Formula and Stokes Formula) 一、高斯公式 二、斯托克斯公式 三、格林公式、高斯公式、 斯托克斯公式之间的关系 四、小结与思考练习 2009年7月27日星期一 2 目录 上页 下页 返回
2009年7月27日星期一 2 目录 上页 下页 返回 第六节 高斯公式 斯托克斯公式 第九章 (Gauss Formula and Stokes Formula) 一、高斯公式 二、斯托克斯公式 三、格林公式 ﹑高斯公式 ﹑ 斯托克斯公式之间的关系 四、小结与思考练习

一、高斯公式(Gauss Formula) 定理1设空间闭区域Ω由分片光滑的闭曲面Σ围成, 函数P(x,y,z)、2(x,y,z)、R(x,y,z)在2上具有一阶连 续偏导数,则有公式 +-月P+0+ j 或P+e+那h=psa+QoB+Ros7as 这里∑是2的整个边界曲面的外侧cosa,cosB,c0sy是 ∑上点(x,y,z)处的法向量的方向余弦. 2009年7月27日星期一 3 目录 上页 下页 、返回
2009年7月27日星期一 3 目录 上页 下页 返回 一、高斯公式 (Gauss Formula) 定理 1 设空间闭区域 Ω由分片光滑的闭曲面 Σ 围成, 函数 P x y z),( 、 xQ y z),( 、 R x y z),( 在 Ω上具有一阶连 续偏导数, 则有公式 ∫∫∫ ∫∫ Ω ∑ ++= ∂ ∂ + ∂ ∂ + ∂ ∂ dv Pdydz Qdzdx Rdxdy z R y Q x P ( ) 这里 ∑ 是 Ω的整个边界曲面的外侧cos α ,cos β ,cosγ 是 ∑上点 x y z),( 处的法向量的方向余弦 . dv RQP dS z R y Q x P ∫∫∫ ( ∫∫ () cos cos cos ) Ω ∑ = ++ ∂ ∂ + ∂ ∂ + ∂ ∂ 或 γβα
证明:设闭区域2在面x0y上的投影区域为Dy ∑由∑,∑,和∑,三部分组成, ∑1:乙=z1(x,y)取下侧 ∑2:?=z,(x,y)取上侧 z4 ∑2:z=32(x,y) ∑?是以闭区域D的 边界曲线为准线,母线平 行于z轴的柱面上的一部 :z=(x,y) 分,取外侧. 2009年7月27日星期一 4 目录 上页 下页 返回
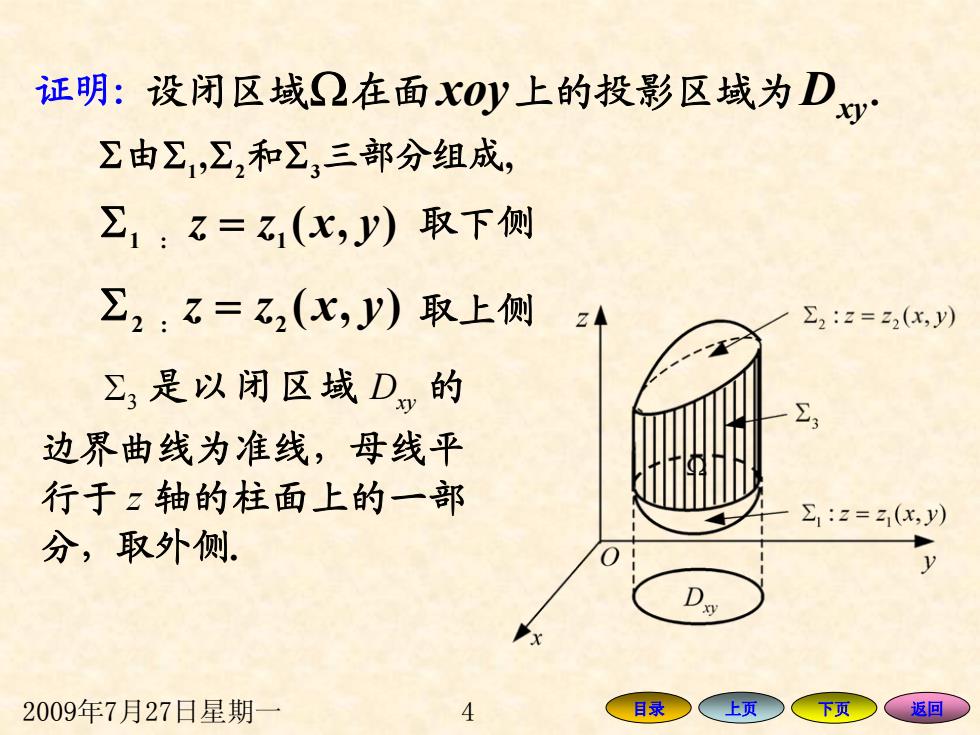
2009年7月27日星期一 4 目录 上页 下页 返回 证明:设闭区域 Ω在面xoy上的投影区域为 Dxy . Σ 由 Σ 1 , Σ 2 和 Σ 3三部分组成 , ),( :1 1 Σ z = z x y ),( :2 2 Σ z = z yx 取下侧 取上侧 Σ 3 是以闭区域 Dxy 的 边界曲线为准线,母线平 行于 z 轴的柱面上的一部 分,取外侧

根据三重积分的计算法 四-w器 ={R[x,y,zz(x,y)]-R[x,y,z(x,y)Bbdxdy. D 根据曲面积分的计算法 R(x,y,z)dxdy=-RIx,y,(x,y)ldxdy, j∬R(x,z)k=∬RIx,八a,(x,yl, ∬R(x,J,z)=0. Σ3 2009年7月27日星期一 5 目录○ (上页 下页 、返回
2009年7月27日星期一 5 目录 上页 下页 返回 根据三重积分的计算法 2 1 (,) (,) { } xy z xy z xy D R R dv dz dxdy z z Ω ∂ ∂ = ∂ ∂ ∫∫∫ ∫∫ ∫ .)]},(,[)],(,[{ = ∫∫ 2 − 1 Dxy dxdyyxzyxRyxzyxR 根据曲面积分的计算法 ),( ,)],(,[ 1 1 ∫∫ ∫∫ −= Σ Dxy dxdyzyxR dxdyyxzyxR 2 2 ( , , ) [ , , ( , )] , Dxy R x y z dxdy R x y z x y dxdy Σ = ∫∫ ∫∫ 3 R x y z dxdy ( , , ) 0. Σ = ∫∫