
新课引入 前面我们讲述了两类曲线积分: 孤长曲线积分(第一类) 坐标曲线积分(第二类)。 同样我们也要讲述两类曲面积分: 对面积的曲面积分(第一类) 对坐标的曲面积分(第二类)。 上一节我们讲述了对面积的曲面积分, 这一节我们就来讲对坐标的曲面积分。 2009年7月27日星期一 目录 上页 下页 返回
2009年7月27日星期一 1 目录 上页 下页 返回 新课引入 前面我们讲述了两类曲线积分: 弧长曲线积分(第一类) 坐标曲线积分(第二类)。 上一节我们讲述了对面积的曲面积分, 这一节我们就来讲对坐标的曲面积分。 同样我们也要讲述两类曲面积分: 对面积的曲面积分(第一类) 对坐标的曲面积分(第二类)

第九章 第五节对坐标的曲面积分 Surface integral of coordinate) 一、对坐标的曲面积分的概念与性质 二、对坐标的曲面积分的计算 三、两类曲面积分之间的联系 四、小结与思考练习 2009年7月27日星期一 2 目录 上页 下页 返回
2009年7月27日星期一 2 目录 上页 下页 返回 第五节 对坐标的曲面积分 第九章 (Surface integral of coordinate) 一、对坐标的曲面积分的概念与性质 二、对坐标的曲面积分的计算 三、两类曲面积分之间的联系 四、小结与思考练习

一、对坐标的曲面积分的概念与性质 1.有向曲面及其在坐标面上的投影概念 观察以下曲面的侧(假设曲面是光滑的) 曲面分上侧和下侧 曲面分内侧和外侧 以后如未作特别说明,我们所讨论的曲面都是双侧的. 2009年7月27日星期一 3 目录 上页 下页 返回
2009年7月27日星期一 3 目录 上页 下页 返回 一、对坐标的曲面积分的概念与性质 1. 有向曲面及其在坐标面上的投影概念 观察以下曲面的侧 (假设曲面是光滑的 ) 曲面分 上侧和 下 侧 曲面分 内侧和 外 侧 以后如未作特别说明,我们所讨论的曲面都是双侧的

曲面法向量的指向决定曲面的侧。 决定了侧的曲面称为有向曲面. 曲面的投影问题:在有向曲面公上取一小块△S 假定AS在xOy面的投影(△S)w为 (△o),c0sy>0 cosy =0 其中(△o)m为投影区域的面积。 2009年7月27日星期一 4 目录 上页 下页 、返回
2009年7月27日星期一 4 目录 上页 下页 返回 曲面法向量的指向决定曲面的 侧 . 决定了侧的曲面称为有向曲面 . 曲面的投影问题 : 在有向曲面 Σ 上取一小块 Δ S 假定 Δ S 在 xOy 面的投影( ) xy Δ S 为 ( ) cos 0 ( ) ( ) cos 0 0 cos 0 xy xy xy S σ γ σ γ γ ⎧ Δ > ⎪ Δ = −Δ < ⎨ ⎪ ⎩ = , , , 其中( ) Δ σ xy 为投影区域的面积
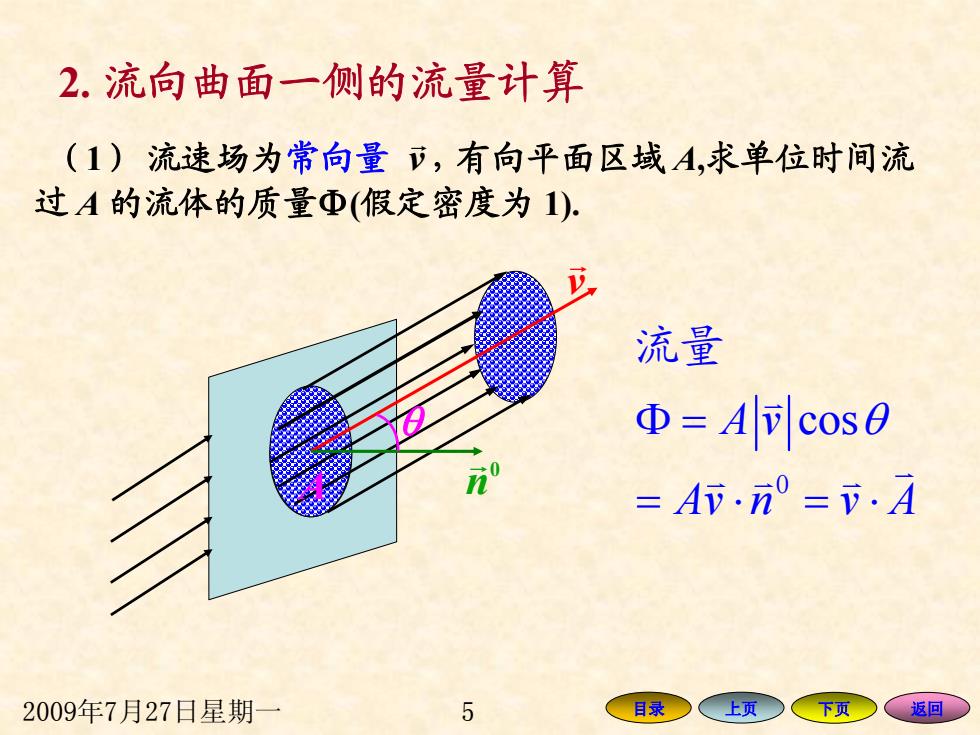
2.流向曲面一侧的流量计算 (1)流速场为常向量立,有向平面区域A,求单位时间流 过A的流体的质量Φ(假定密度为1) 流量 Φ=Acos0 =Av.n=v.A 2009年7月27日星期一 5 目录○ 上页 下页 返回
2009年7月27日星期一 5 目录 上页 下页 返回 2. 流向曲面一侧的流量计算 ( 1 ) 流速场为常向量 v G,有向平面区域 A ,求单位时间流 过 A 的流体的质量 Φ (假定密度为 1). A v G 0 n G θ A 0 A v cos Avn vA Φ = θ = ⋅ =⋅ K K K K K 流量