几何意义当变点z进入z.的充分小的去心邻域时,它的像点)就落入A的一个预先给定的邻域内之平面2w平面7AuaC0定义中z→>zo的方式是任意的,也就是说,z在zo的去心邻域内沿任何曲线以任何方式趋于z时,)都要趋向于同一个常数A
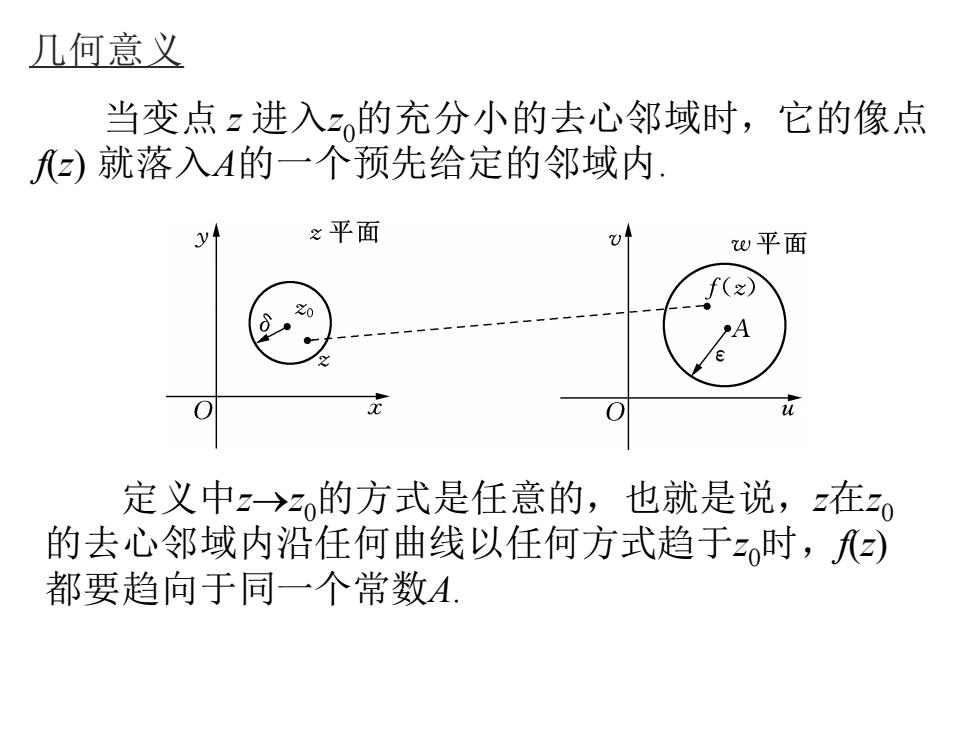
几何意义 当变点 z 进入z0的充分小的去心邻域时,它的像点 f(z) 就落入A的一个预先给定的邻域内. 定义中z→z0的方式是任意的,也就是说,z在z0 的去心邻域内沿任何曲线以任何方式趋于z0时,f(z) 都要趋向于同一个常数A

极限计算的性质设 f(z)=u(x,y)+iv(x,y), A=uo +ivo定理2.1Zo=xo+iyo,那末lim f(z)= A的充要条件是Z>Z0lim u(x, y) =uo lim v(x, y) = Vox-→xox→xoy-→yoy→yo证 (1)必要性如果 lim f(z)= A,根据极限的定义Z→Z0当0<(x+iy)-(x+iyo)<8时,(u+iv) -(uo +ivo)/<8,12
12 极限计算的性质 定理2.1 lim ( , ) , lim ( , ) . , lim ( ) ( ) ( , ) ( , ), , 0 0 0 0 0 0 0 0 0 0 0 0 u x y u v x y v z x iy f z A f z u x y iv x y A u iv y y x x y y x x z z = = = + = = + = + → → → → → 那 末 的充要条件是 设 证 lim ( ) , 0 f z A z z = → 如果 根据极限的定义 0 ( ) ( ) , 当 x + iy − x0 + iy0 时 ( ) ( ) , 0 0 u + iv − u + iv (1) 必要性

或当 0</(x-x)+(y-y)<时,[(u-uo)+i(v-vo)|<, = u-uol<, -vol<8,故 lim u(x,y) =uo,lim v(x, y) = Vox-→xox-→>xoy→yoy-→yo(2) 充分性若 lim u(x,y)=uo lim v(x, y) = Vosx→>xox-→xoy→yoy-→yo那么当 0<(x-x)+(y-yo)<时,88有 u-uo2213
13 0 ( ) ( ) , 2 0 2 或当 x − x0 + y − y 时 ( ) ( ) , 0 0 u − u + i v − v , , 0 0 u − u v − v lim ( , ) , lim ( , ) . 0 0 0 0 0 0 u x y u v x y v y y x x y y x x = = → → → → 故 lim ( , ) , lim ( , ) , 0 0 0 0 0 0 u x y u v x y v y y x x y y x x = = → → → → 若 0 ( ) ( ) , 2 0 2 那么当 x − x0 + y − y 时 (2) 充分性. , 2 , 2 0 0 有 u − u v − v

f(z)-A= (u-uo)+i(v-vo)≤ u-uo+|v-v故当 0<-zol<时,f(z)-A<,所以 lim f(z)= A.[证毕]Z→Zo注:该定理将求复变函数f(z)=u(x,J)+iv(x,y)的极限问题,转化为求两个二元实变函数u(x,J)和v(x,y)的极限问题14
14 ( ) ( ) ( ) 0 0 f z − A = u − u + i v − v 0 0 u − u + v − v 0 , 故当 z − z0 时 f (z) − A , lim ( ) . 0 f z A z z = → 所以 [证毕 ] 注:( , ) . , ( , ) ( ) ( , ) ( , ) 和 的极限问题 的极限问题 转化为求两个二元实变函数 该定理将求复变函数 v x y u x y f z = u x y + iv x y

定理2.2)若(极限运算法则)lim f(z)= A,,limg(z)=B2→202-→20则(l) lim(f(z)±g(z)) = A± B;Z>20(2) lim f(z) · g(z) = AB;2→20Af(α)(3) lim(B ±0)Bg(z)20若两个函数(z)和g(z)在点zo处有极限,则其和、差、积、商(要求分母不为零)在点zo处的极限仍存在,并且极限值等于z)、g(z)在点zo处的极限值的和、差、积、商
定理2.2 (极限运算法则) 若 0 0 lim ( ) , lim ( ) , z z z z f z A g z B → → = = 0 0 0 (1) lim( ( ) ( )) ; (2) lim ( ) ( ) ; ( ) (3) lim ( 0). ( ) z z z z z z f z g z A B f z g z AB f z A B g z B → → → = = = 则 若两个函数f(z)和g(z)在点z0处有极限,则其和、 差、积、商(要求分母不为零)在点z0处的极限仍存在, 并且极限值等于f(z)、g(z)在点z0处的极限值的和、差、 积、商