《线性代数》课程教学课件（PPT讲稿，A）§2.4 矩阵的秩

线性代数 第二章新乐我桃川科$ 2.4矩阵的秩矩阵的行(列)秩、秩矩阵秩的求法二、三、向量组的秩、最大无关组的求法四、k阶子式五、小结上页下页返回

线性代数 第二章 §2.4 矩阵的秩 一、 矩阵的行(列)秩、秩 二、 矩阵秩的求法 三、向量组的秩、最大无关组 的求法 四、 k 阶子式 五、小结 上页 下页 返回

线性代数 第二章我新乐我就科一、矩阵的行(列)秩、秩定义2.4.1设mXn矩阵A，称A的行向量组的秩为矩阵A的行秩，列向量组的秩称为矩阵A的列秩0例1求矩阵A=的行秩和列秩01224解： A的行向量α, =(1,0,1),α, =(0,1,2),α, =(2,1,4)由行列式012=0，知向量组αi,αz,α,线性相关,42

线性代数 第二章 定义2.4.1 设m×n矩阵A，称A 的行向量组的秩为矩阵A的 行秩，列向量组的秩称为矩阵A的列秩. 一、矩阵的行(列)秩、秩 1 0 1 1 0 1 2 . 2 1 4 A     =       例 求矩阵 的行秩和列秩 1 2 3 A的行向量   = = = (1,0,1), (0,1,2), (2,1,4) 1 2 3 1 0 1 0 1 2 0 , , 2 1 4 由行列式 = ，知向量组   线性相关， 解：

线性代数 第二章我新乐装然川科又α,α,线性无关，故α,α,是A的行向量组的一个最大无关组，所以矩阵A的行秩等于2.同样方法可以求出A的列秩等于2１3例2求矩阵A=-1的行秩和列秩，0275000解： A的行向量α, =(1,1,3,1),α, =(0,2,-1,4),αg = (0,0,0,5)去掉第三个分量，得α, =(1,1,1),α, = (0,2,4),α, = (0,0,5)

线性代数 第二章 1 2 1 2 , , 2. A A 又    线性无关，故 是 的行向量组的一个 最大无关组，所以矩阵 的行秩等于 1 2 3 (1,1,3,1), (0,2, 1,4), (0,0,0,5). A    = = − = 的行向量 同样方法可以求出A的列秩等于2. 1 1 3 1 2 0 2 1 4 . 0 0 0 5 A     = −       例 求矩阵 的行秩和列秩 解： 1 2 3       = = = (1,1,1), (0,2,4), (0,0,5). 去掉第三个分量，得

线性代数 第二章教新乐教二料1由行列式0知向量组α,α,α线性无关，24=10±0，500无关组添加则向量组α,α,,α,也线性无关分量仍无关所以A的行秩为3.[131142A的列向量组β,=β, =|-10β, =β=[o][5][o]0而其中βββ4线性无关，4个三维向量必线性相关

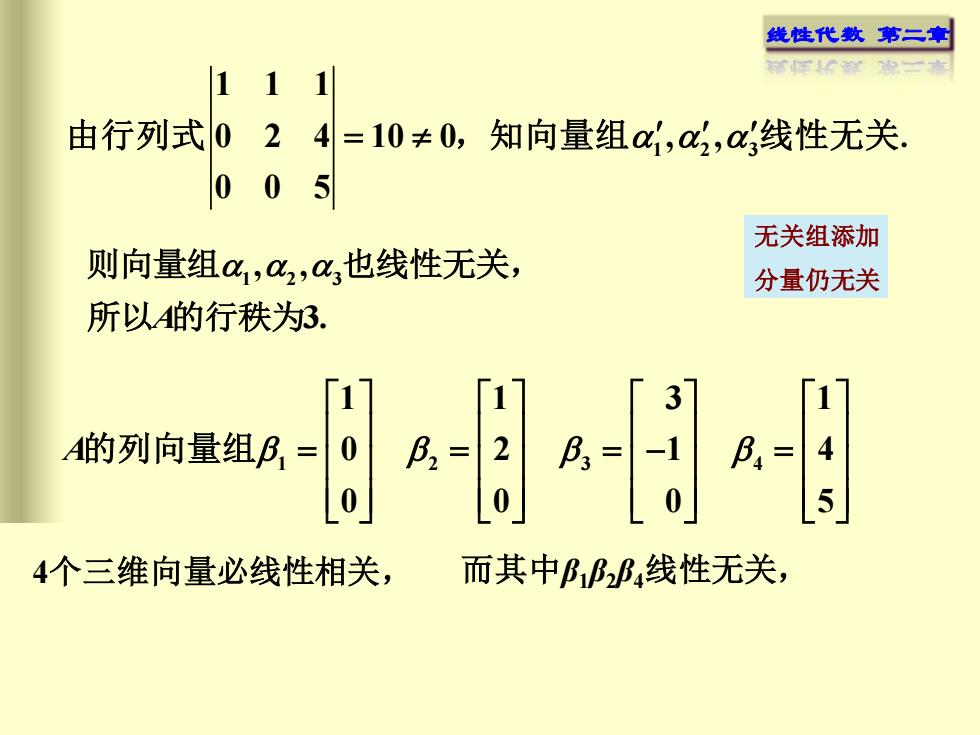
线性代数 第二章 1 2 3 111 0 2 4 10 0 , , 005 由行列式 =  ，知向量组     线性无关. 1 2 3 , , A 3. 则向量组   也线性无关， 所以 的行秩为 1 2 3 4 1 1 3 1 0 2 1 4 0 0 0 5 A                     = = = − =                         的列向量组 4个三维向量必线性相关， 而其中β1β2β4线性无关， 无关组添加 分量仍无关

线性代数 第二章我新我桃科00因为10=10±055所以A的列秩也等于3例1和例2中矩阵的行秩等于列秩并非是偶然的。为了证明这一点，我们有以下两个定理定理2.4.1初等行(列)变换不改变矩阵的行(列)秩证明略

线性代数 第二章 1 0 0 1 2 0 10 0 1 4 5 =  因为 所以A的列秩也等于3. 例1和例2中矩阵的行秩等于列秩并非是偶然的. 为了证明这一点，我们有以下两个定理. 定理2.4.1 初等行(列)变换不改变矩阵的行(列)秩. 证明： 此处只就第三种初等行变换不改变矩阵的 行秩证明之，其余两种课下自己来完成 证明略.