函数W=z?构成的映射例2.1根据复数的乘法公式可知,映射W=,将z的辐角增大一倍+X将z平面上与实轴交角为为α的角形域映射成w平面上与实轴交角为2α的角形域
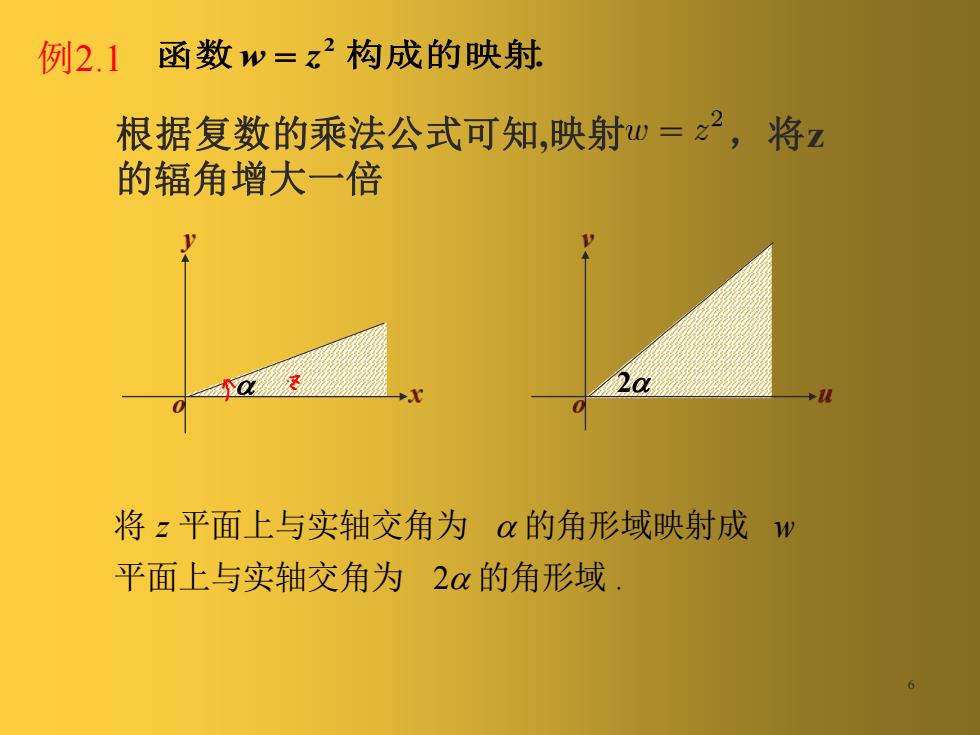
. 函数 w = z 2 构成的映射 2 6 例2.1 根据复数的乘法公式可知,映射 ,将z 的辐角增大一倍 2 . 平面上与实轴交角为 的角形域 将 平面上与实轴交角为 的角形域映射成 z w

例2.2函数w=z将z平面上的三角形变成w平面上的何种曲线?=2±3i·W, =1+2i+l=1-2iwi =2-3i
z 2 3i 1 = + w 2 3i 1 = − z 1 2i 2 = − w 1 2i 2 = + A B C A B C 7 例2.2 函数 w z = 将z平面上的三角形变成w 平面上的 何种曲线?

例2.3函数W==将z平面上的直线x=1变成w平面上2的何种曲线?¥1x-iy解: z=x+iy,w=u+iv= x? + y2x+iyZz平面上的直线x=1对应于w平面上的曲线1yuV1+ y1+ y1u(1+ y)2(1+y)?1=uyt之平面U1+ yw平面cu04=ltC
例2.3 函数 将z平面上的直线x=1变成w 平面上 的何种曲线? 1 w z = 解: 2 2 1 1 i i , i i x y z x y w u v z x y x y − = + = + = = = + + z平面上的直线x=1对应于w平面上的曲线 2 2 1 , 1 1 y u v y y = = − + + 2 2 2 2 2 2 2 2 1 (1 ) (1 ) 1 1 y u v y y u y + = + + + = = + 1 1 2 2 ( ) 2 4 u v − + =

反函数的定义设W=f(z的定义集合为z平面上的集合E,函数值集合为W平面上的集合F=fE),那末F中的每一个点W必将对应着E中的一个或几个点。于是在F上就确定了一个单值或多值)函数,记作:z=f-l(w),它称为函数w=f(z)的反函数,也称为映射W=f(z)的逆映射如果函数(映射)W=f(z)与它的反函数(逆映射)z =Φ(W)都是单值的那末称函数(映射)W=f(z)是一一对应的也可称集合E与集合F是一一对应的
反函数的定义 ( ) . ( ), ( ) , 每一个点 必将对应着 中的一个 或几个 点 数值集合为 平面上的集合 那 末 中 的 设 的定义集合为 平面上的集合 函 w E w F f E F w f z z E = = ( ) . ( ), ( ) , ( ) , 1 为映射 的逆映射 它称为函数 的反函数 也 称 于是在 上就确定了一个单值或多值 函 数 w f z z f w w f z F = = = − 记作: 9 . ) ( ) . ( ) ( ) , ( ( ) ( ) 合 是一一对应的 射 是一一对应的也可称集合 与 集 逆映射 都是单值的那末称函数 映 如果函数 映 射 与它的反函数 F w f z E z w w f z = = =

$ 2.1.2复变函数的极限定义2.2设函数w=(z)定义在z.的去心邻域0<z-zo<r内若存在常数A,对于任意给定0的,都存在一正数8(0<&r),使得当0<z-zo< r时,有[f(z)-A|<,则称函数(z)当z→>z.时的极限存在,常数A为其极限值记作lim f(z) = AZ>20或 f(2) → A(z →z).以我为心,心中无我虚怀若谷,放眼苍穹
§2.1.2 复变函数的极限 定义2.2 设函数w=f(z)定义在z0的去心邻域0<|z-z0 |<r内, 若存在常数A,对于任意给定<0的,都存在一正数 (0<r),使得当0<|z-z0 |< r时,有 , 则称函数f(z)当z→z0时的极限存在,常数A为其极限值. 记作 或 . f z A ( ) − 0 lim ( ) z z f z A → = 0 f z A z z ( ) ( ) → → 以我为心,心中无我 虚怀若谷,放眼苍穹