
第六章第二节定积分在几何学上的应用平面图形的面积二、体积三、平面曲线的弧长
二、体积 第二节 一、 平面图形的面积 三、 平面曲线的弧长 定积分在几何学上的应用 第六章
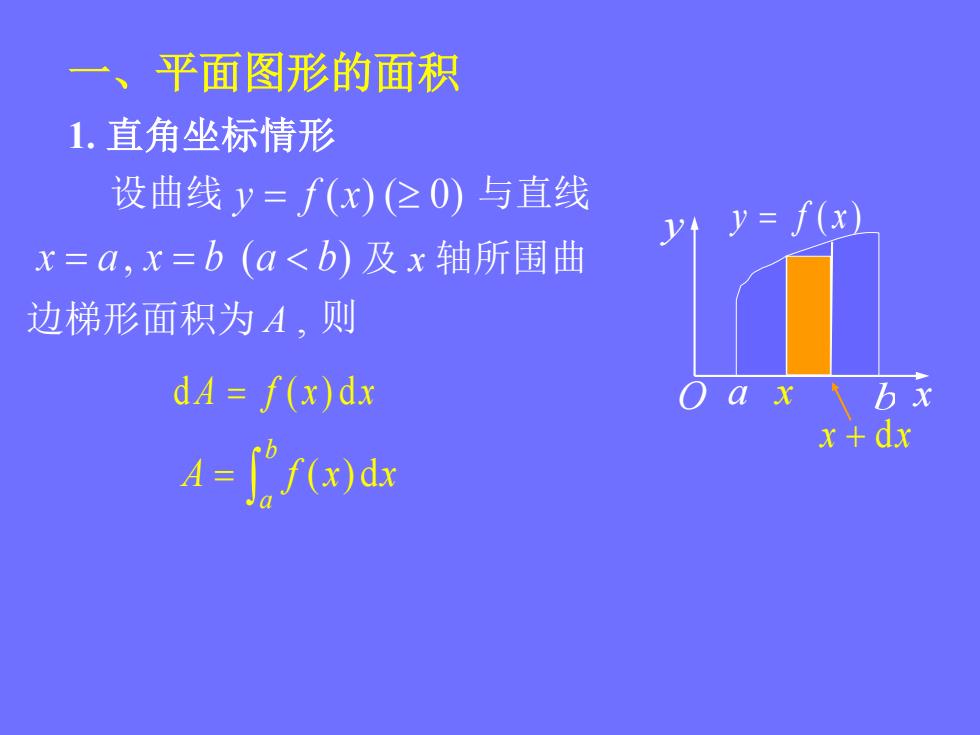
一、平面图形的面积1.直角坐标情形设曲线y=f(x)(≥0)与直线yt y= f(x)x=a,x=b(a<b)及x轴所围曲边梯形面积为A,则dA = f(x)dxOaxbxx+dxA= J" f(x)dx
一、平面图形的面积 1. 直角坐标情形 设曲线 与直线 及 x 轴所围曲 则 dA f ( x) dx A f x x b a ( ) d 边梯形面积为 A , O a b x y y f ( x ) x dx x
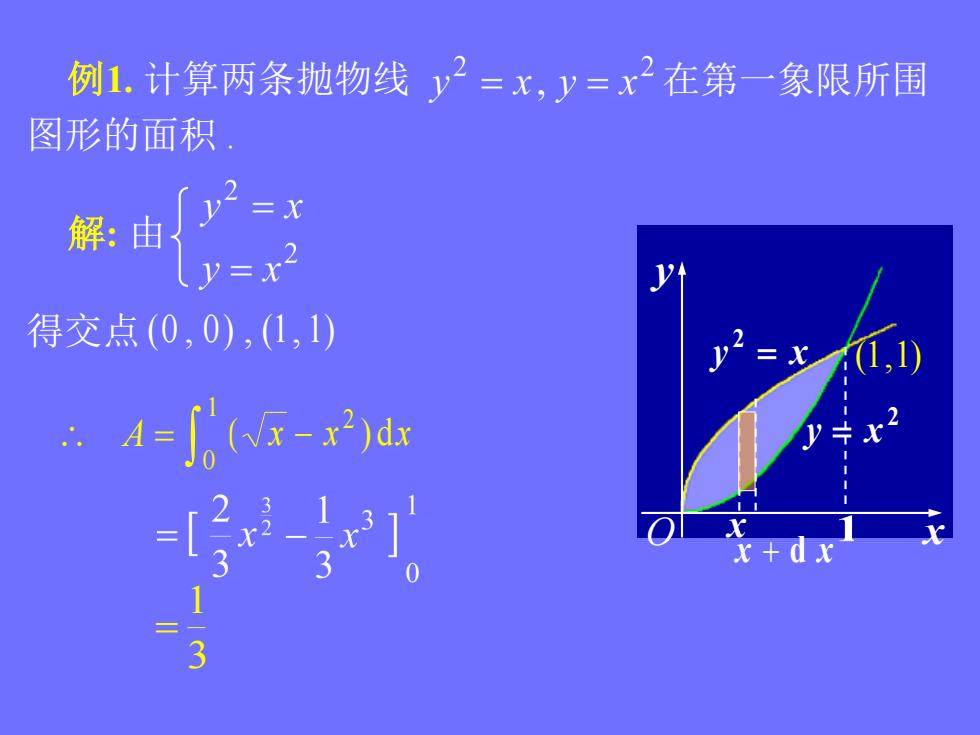
例1.计算两条抛物线2=x,=x2在第一象限所围图形的面积解:由得交点(0,0),(1,1)y2 =x (1,1)A=(Vx-x2)dxAx+dx
例1. 计算两条抛物线 在第一象限所围 图形的面积 . 解: 由 得交点 (0 , 0) , (1, 1) d A ( x x ) dx 2 3 1 1 0 A x y O y x 2 2 y x x x d x (1,1) 1

例2.计算抛物线y2=2x与直线y=x-4所围图形的面积=2x得交点解:由y2 = 2x8,4)y=x-4V+((2, -2), (8, 4)为简便计算,选取V作积分变量?=x-4则有2.-[, (y+ 4-1y2)dyA=I=[22 +4y-13 ]42 = 18
O y 2x 2 y x 4 x y 例2. 计算抛物线 y 2x 2 与直线 的面积 . 解: 由 得交点 (2 , 2) , (8 , 4) (8 , 4) d A ( y 4 y ) d y 2 2 1 18 y x 4 所围图形 (2 , 2) 为简便计算, 选取 y 作积分变量, 则有 4 2 A y y d y
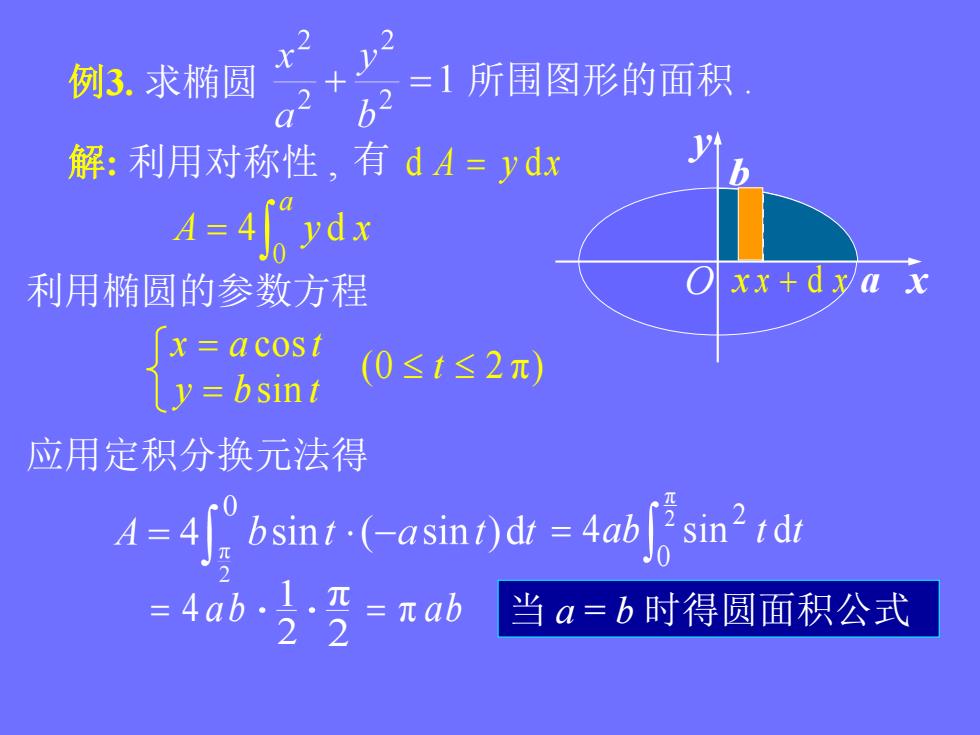
=1所围图形的面积例3.求椭圆6V解:利用对称性,有 dA=ydxA= 4fydxxx+dxax利用椭圆的参数方程x=acost(0≤t≤2元)y=bsint应用定积分换元法得sin'tdtbsint (-asint)dt = 4ab=4ab.1.元=元ab当a=b时得圆面积公式22
a b 例3. 求椭圆 解: 利用对称性 , d A y dx 所围图形的面积 . 有 a A y x 0 4 d 利用椭圆的参数方程 (0 2 π ) sin cos t y b t x a t 应用定积分换元法得 2 π 0 2 4ab sin t dt 4 ab 2 1 2 π π ab 当 a = b 时得圆面积公式 x x d x x y O