《高等数学》课程教学资源（课件讲稿）第七章 微分方程_7-5 可降阶高阶微分方程

第七章第五节可降阶高阶微分方程一、 (n) = f(x)型的微分方程二、"=f(x,)型的微分方程三、J"=f(y,J)型的微分方程

可降阶高阶微分方程 第五节 一、 型的微分方程 二、 型的微分方程 三、 型的微分方程 第七章

一、y(n)= f(x)型的微分方程令==(-1),则=(m)=f(x),因此dxz =[ f(x)dx+Ci即J(n-1) = [ f(x)dx+C同理可得 y(n-2) =[[J f(x) dx+C, Jdx+C2= JJ f(x)dx Jdx +Cix+C2依次通过n次积分，可得含n个任意常数的通解

一、 ( ) ( ) y f x n  令 , ( 1)  n z y 因此 1 z   f (x)dx  C 即 同理可得   2 ( 2) y dx C n      dx   依次通过 n 次积分, 可得含 n 个任意常数的通解 . 1 C2  C x  型的微分方程

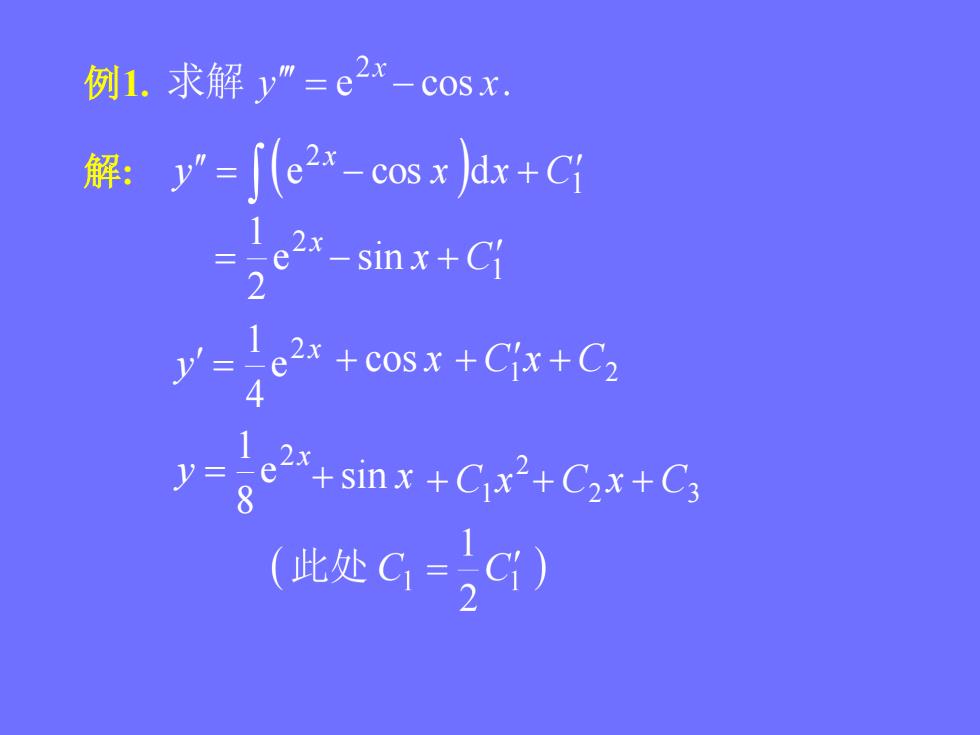
例1.求解 y" =e2x-cos x.解: y"= [(e2x-cos x)dx+Ci- sin x + Ci2x +cos x +Cx+C2+ sin x + Cix?+C2x + C38(此处Ci=Ci)

例1. 解:   1 2 y e cos x dx C x       1 2 e sin 21 x C x     x y 2 e 41   x y 2 e 81   sin x 2 1  C x 2 C3  C x   cos x 1 C2  Cx 

二、"=f(x,y）型的微分方程设 y'=p(x),则y"=p,原方程化为一阶方程p'= f(x, p)设其通解为寸p=β(x,C)则得y' = β(x,C)再一次积分，得原方程的通解y= [p(x,Ci)dx+C2

y   f (x, y ) 型的微分方程 设 y   p (x) , 原方程化为一阶方程 设其通解为 ( , ) C1 p   x 则得 ( , ) C1 y    x 再一次积分, 得原方程的通解 1 2 y   (x,C )dx  C 二

[(1+x2)y"=2xy'例2.求解Jx=0 =1，|x=0=3解：设 '= p(x),则y"= p',代入方程得dp2xdx分离变量(1 +x2)p' = 2xpp(1+x2)积分得 Inp|=ln(1+x2)+lnlC l,即p=C(1+x2)利用 |x=0 =3,得 Ci=3,于是有 y'=3(1+x2)两端再积分得=x3+3x+C2利用 |x=0 =1,得 C2 =1,因此所求特解为y=x3 +3x+1

例2. 求解 (1 x )y   2xy  2 1, y x 0  3 y  x 0  解: 代入方程得 (1 x )p 2x p 2    分离变量 积分得 ln ln (1 ) ln , 1 2 p   x  C 3 , 利用 y  x 0  3, 得 C1  于是有 3(1 ) 2 y    x 两端再积分得 2 3 y  x  3 x  C 利用 1, y x 0  1, 得 C2  3 1 3 y  x  x  因此所求特解为