
第六章第一节定积分的元素法一、什么问题可以用定积分解决?二、如何应用定积分解决问题?
第一节 定积分的元素法 一、什么问题可以用定积分解决 ? 二 、如何应用定积分解决问题 ? 第六章

定积分的元素法通过对不均匀量(如曲边梯形的面积,变速直线运动的路程)的分析,采用“分割、近似代替求和、取极限”四个基本步骤确定了它们的值并由此抽象出定积分的概念,我们发现,定积分是确定众多的不均匀几何量和物理量的有效工具。那么,究竟哪些量可以通过定积分来求值呢?我们先来回顾一下前章中讲过的方法和步骤
通过对不均匀量(如曲边梯形的面积,变速直 线运动的路程)的分析,采用“分割、近似代替 、求和、取极限”四个基本步骤确定了它们的值 ,并由此抽象出定积分的概念,我们发现,定积 分是确定众多的不均匀几何量和物理量的有效工 具。那么,究竟哪些量可以通过定积分来求值呢 ?我们先来回顾一下前章中讲过的方法和步骤。 定积分的元素法
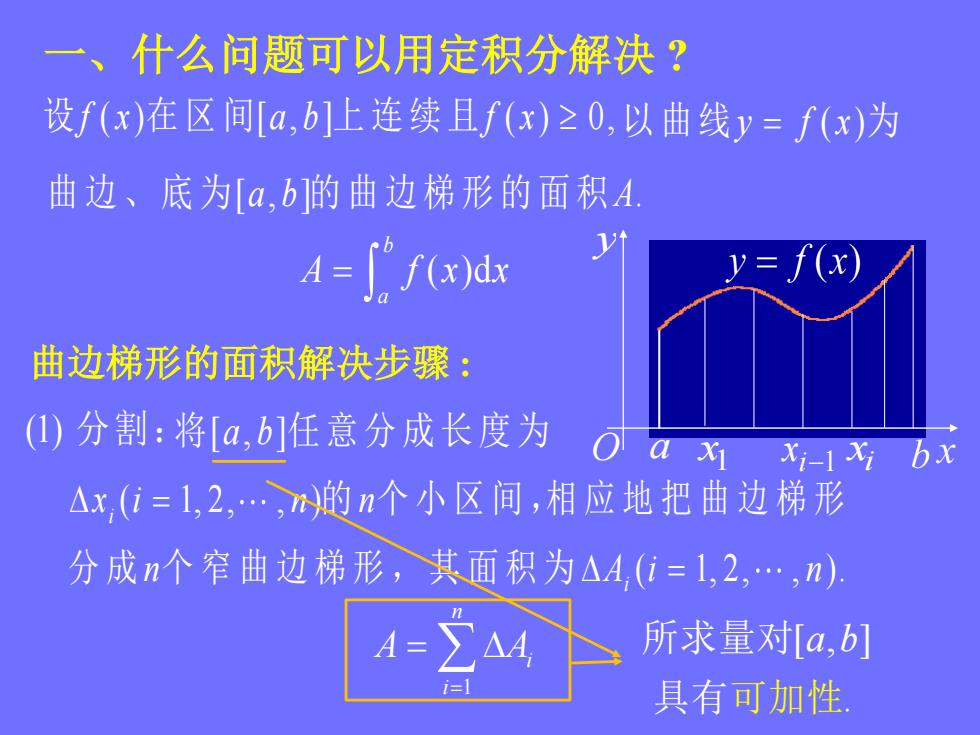
一、什么问题可以用定积分解决?设f(x)在区间[a,b]上连续且f(x)≥0,以曲线y=f(x)为曲边、底为[a,b的曲边梯形的面积AVy=f(x)A= f° f(x)dx曲边梯形的面积解决步骤:(1)分割:将[a,b]任意分成长度为oaxixi-ixibx△xi=1,2,,m的n个小区间,相应地把曲边梯形分成n个窄曲边梯形,其面积为△A(i=1,2,,n)所求量对[a,b]A=ZM,具有可加性
设 f x a b f x ( ) [ , ] ( ) 0, 在 区 间 上 连 续 且 以曲线y f x ( )为 曲 边 、 底 为[ , ] . a b A 的 曲 边 梯 形 的 面 积 ( )d b a A f x x 一、什么问题可以用定积分解决 ? 曲边梯形的面积解决步骤 : (1) 分割:将[ , ] a b 任 意 分 成 长 度 为 ( 1, 2, , ) i x i n n 的 个 小 区 间 ,相 应 地 把 曲 边 梯 形 ( 1, 2, , ). i 分 成 n A i n 个 窄 曲 边 梯 形 , 其 面 积 为 1 n i i A A 1 x i x i1 a x y O [ , ] . 所求量对 a b 具有可加性
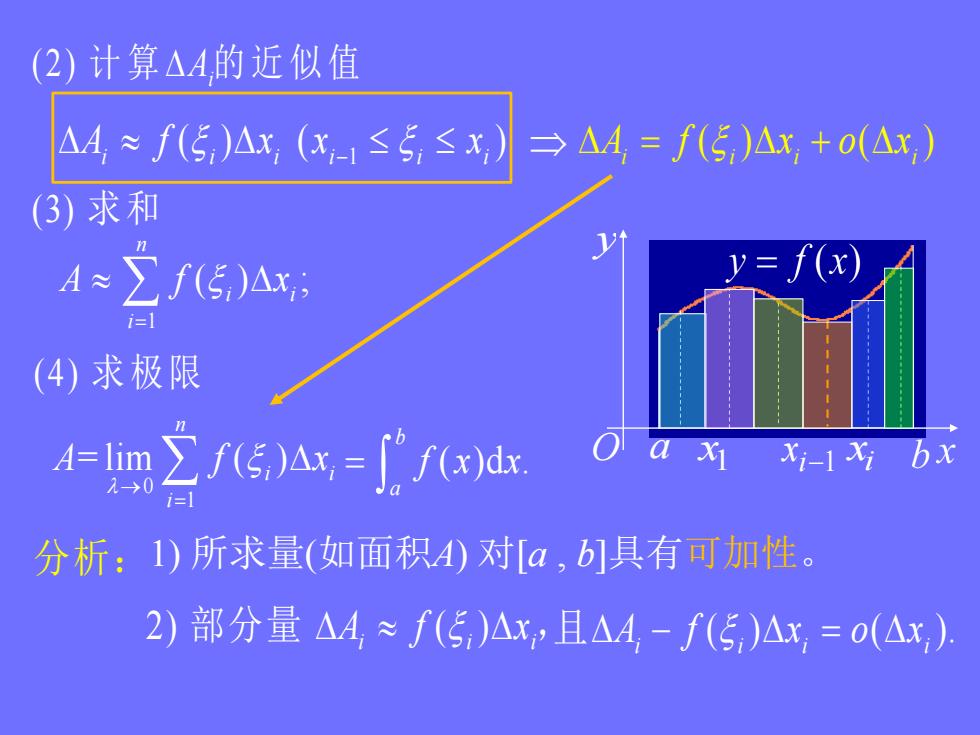
(2)计算△A的近似值AA = f(E)Ax,(xi-≤E,≤x= AA, = f(E)Ax, +o(△x)(3)求和y= f(x)A ~Zf(5)Ax;i=1(4)求极限1Olaxixi-ixibxZ(E)Ax,= [" f(x)dx.A=lim1-0i=1分析:1)所求量(如面积A)对[α,b]具有可加性。2)部分量AA (E)Ax,且△A,-f(E)Ax,=0(△x)
(2) 计 算 Ai 的 近 似 值 1 x i x i1 a x y O 1 ( ) ( ) A f x x x i i i i i i (3) 求和 1 ( ) ; n i i i A f x (4) 求极限 0 1 = lim ( ) n i i i A f x ( )d . b a f x x ( ) ( ) A f x o x i i i i 分析: 1) 所求量(如面积A) 对[a , b]具有可加性。 2) ( ) A f x i i i 部分量 , ( ) ( ). A f x o x i i i i 且

探讨:曲边梯形的面积A=f(x)dx首先将区间[a,b份成n个小区间,取其中任一小区间并记作[xx+dxl,用△A表示其面积y=f(x)A=ZM用取[x,x+dx的左端点x为,以点xdA处的函数值f(x)为高、dx为底的矩形xx+dxbx福的面积f(x)dx为△A的近似值,即SAA~f(x)dx我们把上式右端f(x)dx叫做面积元素,记为dA,即dA=f(x)dx = A=[~ f(x)dx
探讨:曲边梯形的面积A ( )d . b a f x x 首先将区间[ , ] a b n 分成 个小区间,取其中任一小区间并 记作 [ , d ] x x x , a y O x x x d A 用A表示其面积. 用取[ , d ] x x x x 的左端点 为,以点x 处的函数值f x x ( ) d 为高、 为底的矩形 的面积f x x A ( )d 为 的近似值,即 A f x x ( )d A A 我们把上式右端f x x A ( )d 叫做面积元素,记为d ,即 dA f x x = ( )d = ( )d b a A f x x dA