《高等数学》课程教学资源（课件讲稿）第三章课件_第三章第六节

第三章第七节孤微分与曲率弧微分曲率二、三、曲率半径与曲率圆HIGH EDUCATION PRESS机动目录上页下页返回结束

第七节 机动 目录 上页 下页 返回 结束 一、 弧微分 二、 曲率 三、 曲率半径与曲率圆 弧微分与曲率 第三章

曲线的弯曲程度与切线的转角有关与曲线的弧长有关MMMAαHIGHEDUCATION PRESS机动目录上页返回下页结束

曲线的弯曲程度 与切线的转角有关 与曲线的弧长有关 机动 目录 上页 下页 返回 结束  M  M M 

弧微分一、AB设 =f(x)在(α,b)内有连续导数, 其图形为Vy= f(x)弧长 s= AM = s(x)BMMMAsMM'MAxMMAxAxMM'(△x)? +(Ay)xOtbxMM'△xx+△xMM'MM'lim=±1MM'MM'Ax-0= /1+(y): s(x)= limAx-0 △xHIGH EDUCATION PRESS机动目录上页下页返回结束

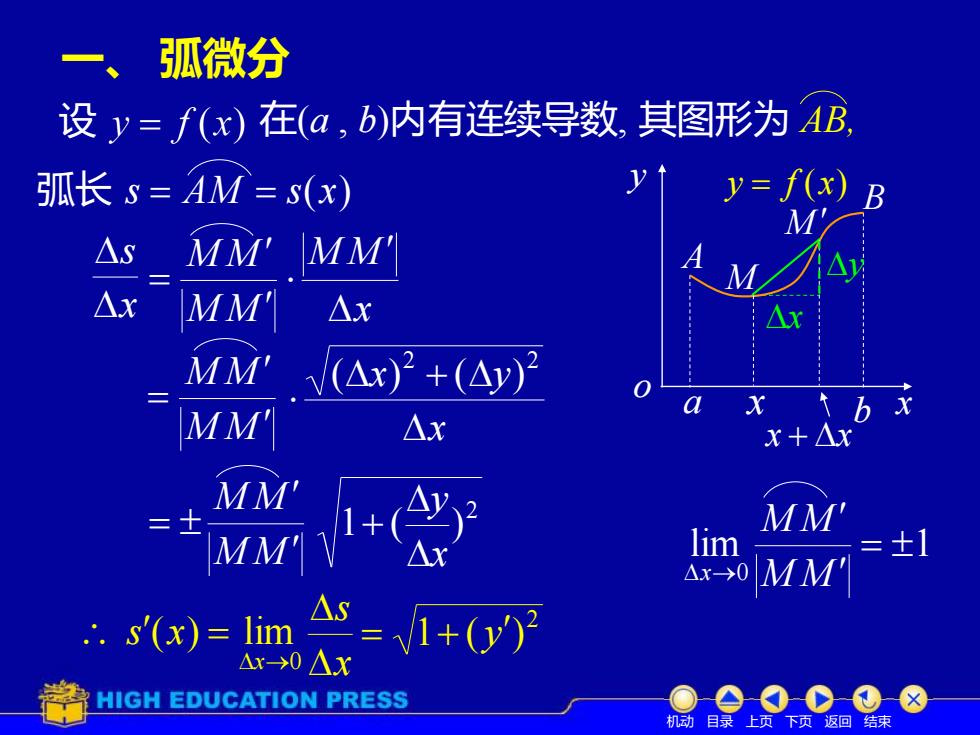
一、 弧微分 设 在(a , b)内有连续导数, 其图形为 AB, 弧长 s = AM = s(x) x s   M M M M   = x M M    M M M M   = x x y   +   2 2 ( ) ( ) M M M M   =  2 1 ( ) x y   + x s s x x     =  →0 ( ) lim 2 = 1+ ( y ) x A B y = f (x) a b x o y x M x + x M  y lim 1 0 =     → M M M M x 机动 目录 上页 下页 返回 结束

s'(x)= /1+(y)x 或 ds = /(dx)2 +(dy)2ds = /1+(y)?dxx= x(t)若曲线由参数方程表示(y= y(t)则弧长微分公式为V(x)" +(y) dtds=V几何意义：ds =|MTayMdxdxQ= sinα= cosα ;dsx x+dxdsXHIGH EDUCATION PRESS机动目录上页下页返回结束

则弧长微分公式为 ( ) ( ) 2 2 d d s x y t = +   ds 1 ( y ) dx 2  = +  或 2 2 ds = (dx) + (dy) x + dx dx o x y x M dy T  几何意义: ds = MT cos ; d d =  s x sin d d = s y 若曲线由参数方程表示:    = = ( ) ( ) y y t x x t 机动 目录 上页 下页 返回 结束

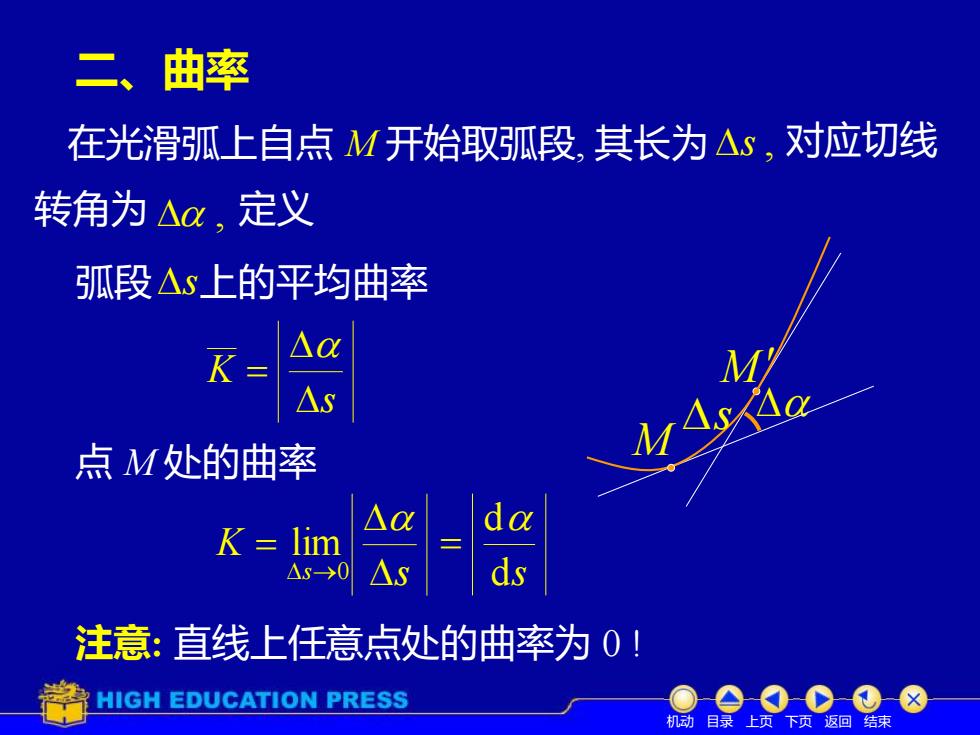
二、曲率在光滑弧上自点 M开始取弧段,其长为△s，对应切线转角为△α，定义弧段△s上的平均曲率1aKMMAAa点M处的曲率AadaK = limAs-0注意：直线上任意点处的曲率为0！HIGHEDUCATIONPRESS机动目录上页下页返回结束

二、曲率 在光滑弧上自点 M 开始取弧段, 其长为 s , 对应切线  , 定义 弧段 s 上的平均曲率 s K   =   M M  s 点 M 处的曲率 s K s   =  →  0 lim ds d = 注意: 直线上任意点处的曲率为 0 ! 机动 目录 上页 下页 返回 结束 转角为