
第九章多元函数微分法及其应用第一节多元函数的基本概念一、平面点集二、多元函数概念三、多元函数的极限四、多元函数的连续性08
第九章 多元函数微分法及其应用 第一节 多元函数的基本概念

平面点集1、平面点集平面点集(1)二元有序实数组(xJ)的全体,即R2=R×R=((x,y)[x,yER)表示坐标平面坐标平面上具有某种性质P的点的集合,称为平面点集,记作E =((x,y)I(x,y)具有性质 P)如C = ((x,y)|x2 + y?<r"}, C=(PIoPl<r).000不不不高等数学教学部不不不
高等数学教学部 2 C {P | OP r}
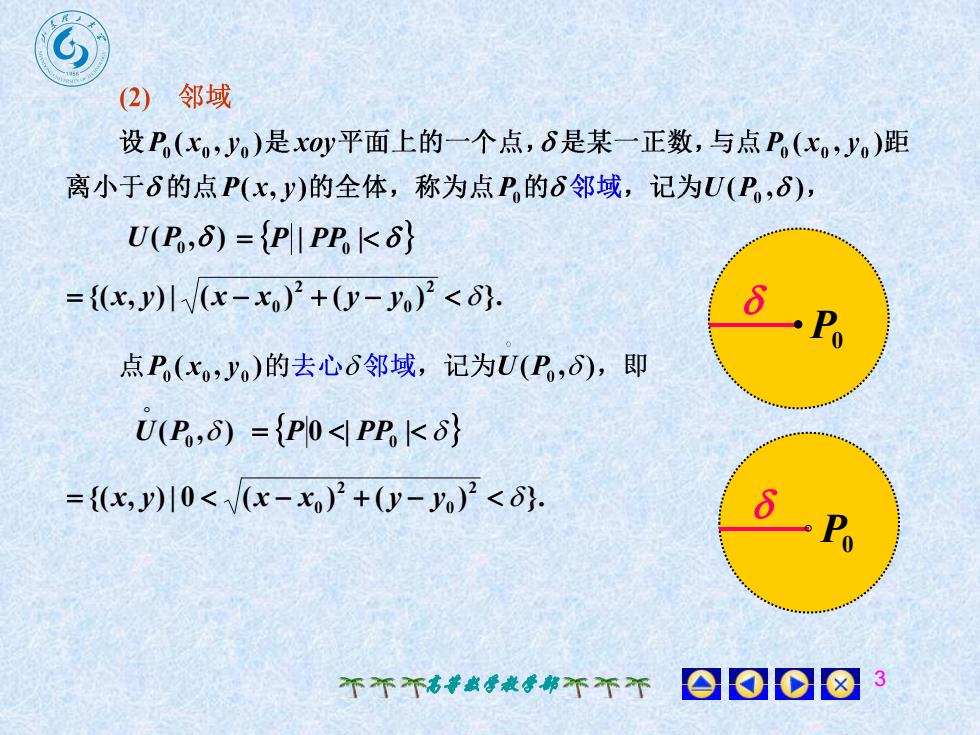
6(2)邻域设P(x,,y)是xoy平面上的一个点,S是某一正数,与点P(xo,y)距离小于S的点P(x,y)的全体,称为点P的S邻域,记为U(P,),U(P,8) = (Pl/PP, <8)=((x,y)/ /(x-x) +(y- yo) <8)SPo点P(x,yo)的去心S邻域,记为U(P,),即U(P,) = (Pl0 </ PP, <8)=((x,y)l0 </(x-x,) +(y- yo) <8)SP0008个个个高数学教学部不不不
高等数学教学部 3 P0 ( , ) U P0 P | PP0 | {( , )| ( ) ( ) }. 2 0 2 x y x x0 y y ( , ) U P0 P 0 | PP0 | {( , )| 0 ( ) ( ) }. 2 0 2 x y x x0 y y P0
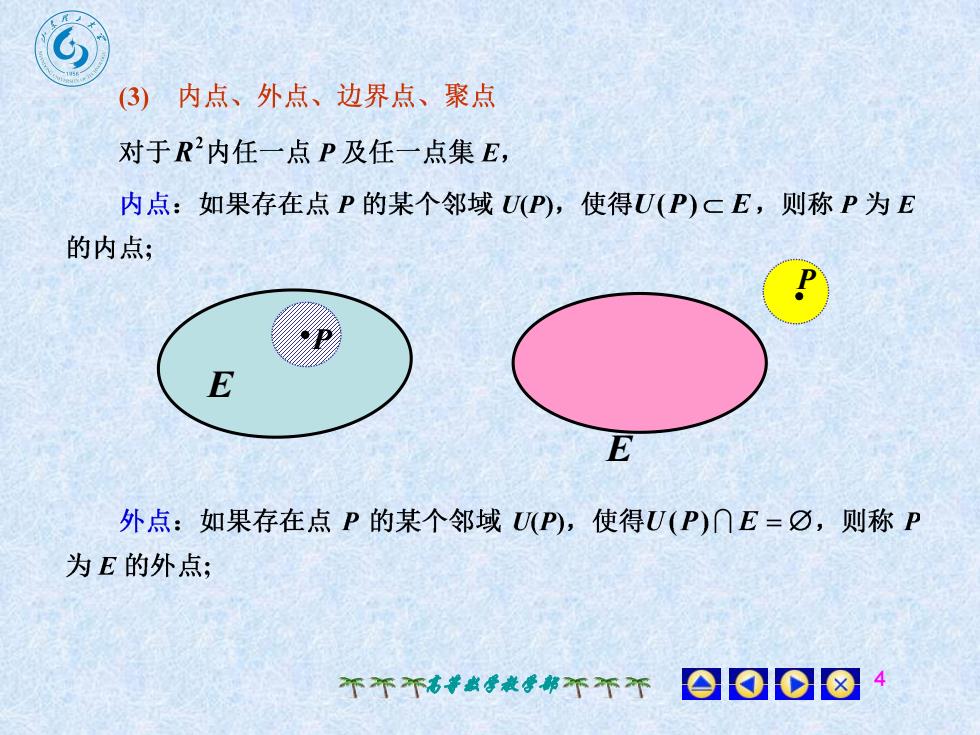
?内点、外点、边界点、聚点(3)对于R2内任一点P及任一点集E,内点:如果存在点P的某个邻域U(P),使得U(P)CE,则称P为E的内点;EE外点:如果存在点P的某个邻域 U(P),使得U(P)OE=O,则称P为E的外点;001018个个个高等数学教学部个不个
高等数学教学部 4 E P E P
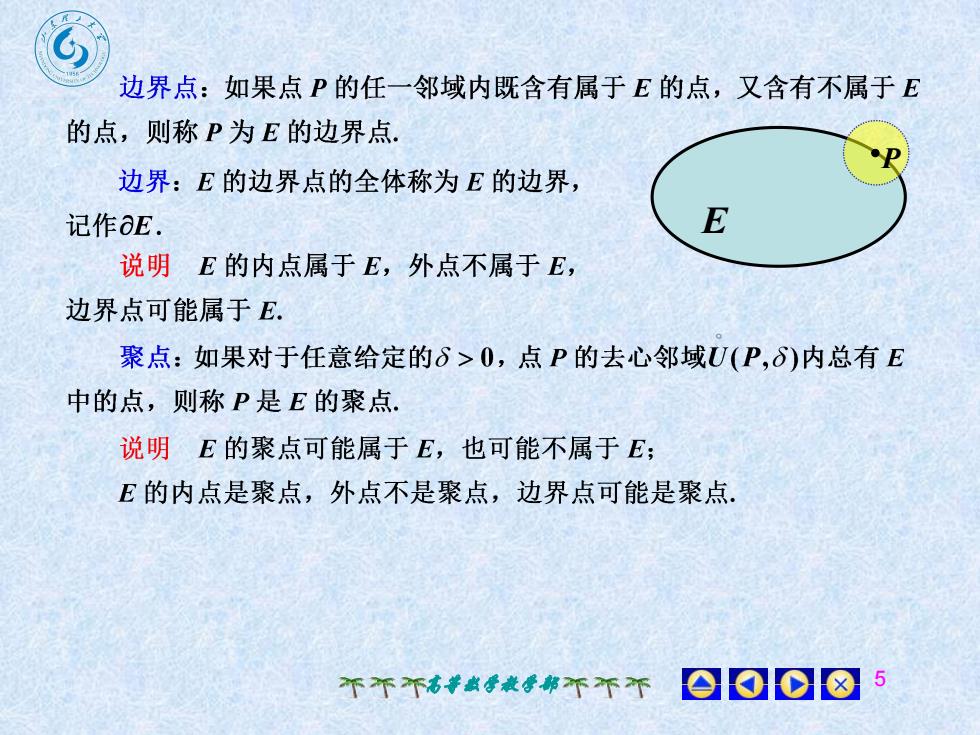
?边界点:如果点P的任一邻域内既含有属于E的点,又含有不属于E的点,则称P为 E的边界点'P边界:E的边界点的全体称为E的边界E记作E.说明 E的内点属于 E,外点不属于E,边界点可能属于E聚点:如果对于任意给定的S>0,点P的去心邻域U(P,S)内总有E中的点,则称P是E的聚点说明E 的聚点可能属于 E,也可能不属于E;E的内点是聚点,外点不是聚点,边界点可能是聚点008个不个高等数学教学部不不个
高等数学教学部 5 E P