
第八章向量代数与空间解析几何第六节空间曲线及其方程空间曲线的一般方程空间曲线的参数方程国三、空间曲线在坐标面上的投影08
第八章 向量代数与空间解析几何 第六节 空间曲线及其方程 一、空间曲线的一般方程 二、空间曲线的参数方程 三、空间曲线在坐标面上的投影
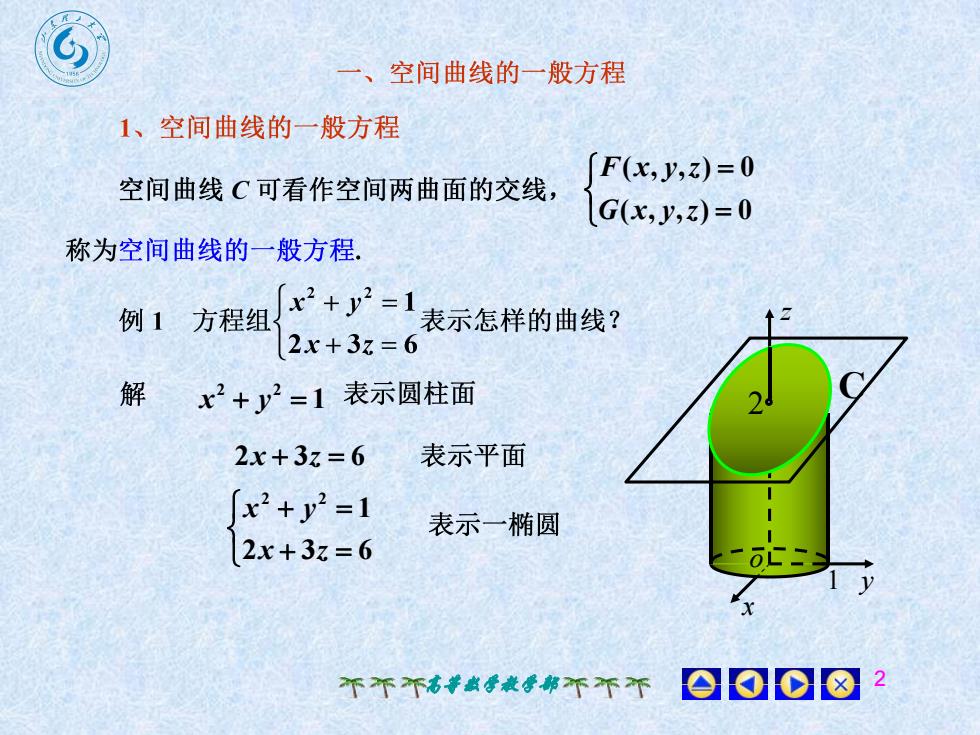
、空间曲线的一般方程1、空间曲线的一般方程[F(x,y,z) =0空间曲线C可看作空间两曲面的交线G(x,y,z)= 0称为空间曲线的一般方程x2 + y2 =1例 1 方程组表示怎样的曲线?2x+3z= 6解 2+y2=1 表示圆柱面2表示平面2x + 3z = 6[x? + y2 =1表示一椭圆2x+3z = 6OL0个个个高数学教学部不不个
高等数学教学部 2 ( , , ) 0 ( , , ) 0 G x y z F x y z 1 2 2 x y 2x 3z 6 2 3 6 1 2 2 x z x y x z 1 y o C 2
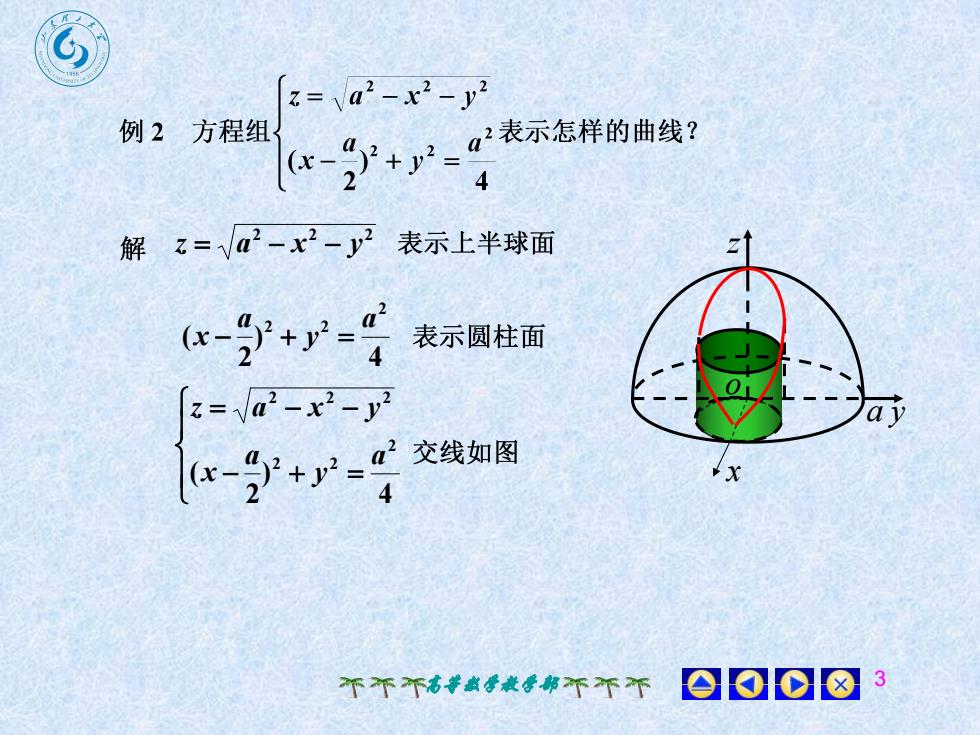
z=a2-x2-y2例 2 方程组[a-+_g表示怎样的曲线?4解 z=a2-x2-y2表示上半球面z1-gy+y-a表示圆柱面z=a2-x?-y?ai2+=交线如图(x-=)xA30008个个个高等数学教学部
高等数学教学部 3 2 2 2 z a x y 4 ) 2 ( 2 2 2 a y a x 4 ) 2 ( 2 2 2 2 2 2 a y a x z a x y y x z a o

二、空间曲线的参数方程x=p(t)空间曲线的参数方程y=y(t),当给定t=t,时,就得到曲线上的一个点z. = (t)(x,,z),随着参数的变化可得到曲线上的全部点001018个不个高等数学教学部不不个
高等数学教学部 4
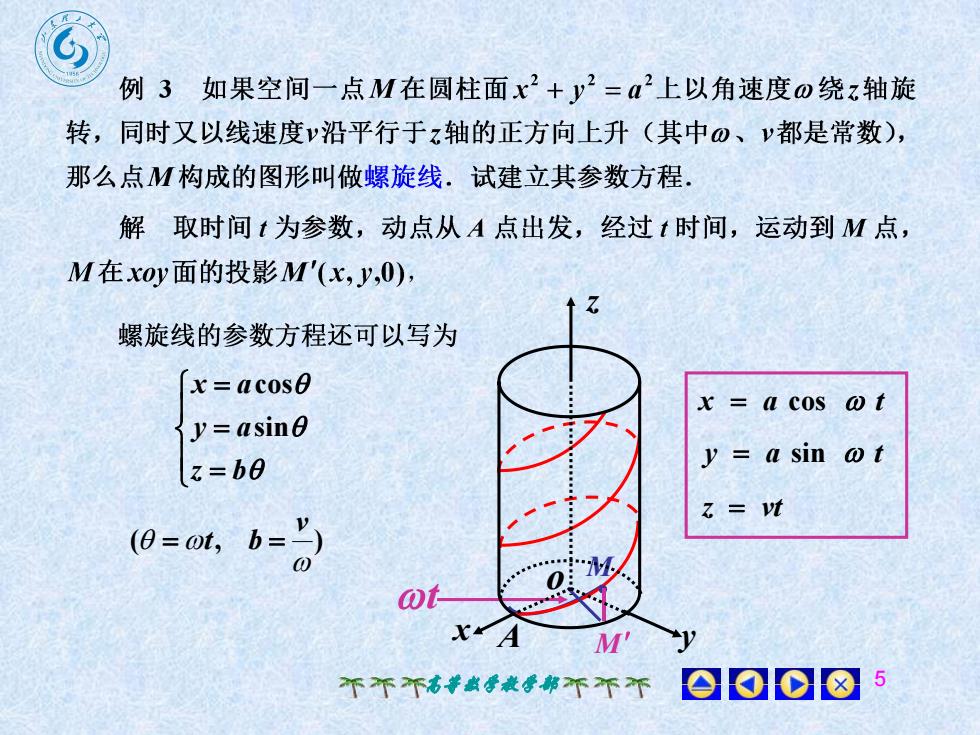
例3如果空间一点M在圆柱面x2+2=a2上以角速度の绕z轴旋转,同时又以线速度v沿平行于z轴的正方向上升(其中の、V都是常数),那么点M构成的图形叫做螺旋线,试建立其参数方程解取时间t为参数,动点从A 点出发,经过t时间,运动到M点,M在xoy面的投影M'(x,y,0)7螺旋线的参数方程还可以写为x=acosox=atacosy=asiney= a sin ot(z=be= vt之(0 = ot, b= =)0otXAM008不不不高尊数学教学部不不不
高等数学教学部 5 x a cos t y a sin t z vt A MM t x y z o z b y a x asincos ( , ) v t b