
第八章向量代数与空间解析几何第五节曲面及其方程曲面研究的基本问题旋转曲面三、柱面四、二次曲面08
第八章 向量代数与空间解析几何 第五节 曲面及其方程 一、曲面研究的基本问题 二、旋转曲面 三、柱面 四、二次曲面

曲面研究的基本问题福曲面研究的基本问题:已知一曲面作为点的几何轨迹时,建立这曲面的方程;(1)(2)已知坐标x,y,z间的一个方程时,研究这方程所表示的曲面的形状.1、建立曲面方程例 1 建立球心在点M,(xo,Jo,z)、半径为R的球面方程解设M(x,J,z)是球面上任一点,根据题意有IMM。=R,(x-x,) +(y-yo)" +(z -zo)~ = R,(x-x)° +(y- yo)2 +(z- z) = R2,球面的标准方程球心在原点时方程为x? + y?+z? = R?.001018中个不个高等数学教学部不不个
高等数学教学部 2 | | , MM0 R ( ) ( ) ( ) , 2 0 2 0 2 x x0 y y z z R ( ) ( ) ( ) , 2 2 0 2 0 2 x x0 y y z z R . 2 2 2 2 x y z R

S例 2 求与原点0及M,(2,3,4)的距离之比为1:2的点的全体所组成的曲面方程IMO|解设M(x,J,z)是曲面上任一点,依题意得IMM,12x+y+z?Vx-2)+(0-3)+(z-4)2agy+1+y-1.所求方程为9例 3 已知A(1,2,3),B(2,-1,4),求线段AB的垂直平分面的方程解设M(x,y,z)是曲面上任一点,依题意得 「MA}=|MBI,/(x-1) +(y-2) +(z-3) = /(x-2) +(y+1) +(z-4)所求方程为 2x -6y + 2z - 7 = 0.001018福个不高等数学教学部不不不
高等数学教学部 3 , 2 1 | | | | 0 MM MO , 2 1 2 3 4 2 2 2 2 2 2 x y z x y z . 9 116 ) 3 4 ) ( 1) ( 3 2 ( 2 2 2 x y z | MA|| MB |, 2 2 2 x 1 y 2 z 3 2 1 4 , 2 2 2 x y z 2x 6 y 2z 7 0

S2、确定方程曲面的形状例 4 方程x2+y2+z2+Ax+By+Cz+F =0表示什么样的曲面?解 此为球面的一般方程,配方得D2+ E2+F2 -4G(x+)+(y+)+(2+)124DEF军当D2+E2+ F2-4G>0时,方程表示球面,球心(-解n2D2+ E2+ F2 - 4G半径为2福H当D2+ E2+ F2-4G =0时,方程表示一点(o不不个高等数学教学部不不个
高等数学教学部 4 , 4 4 ) 2 ) ( 2 ) ( 2 ( 2 2 2 2 2 F 2 D E F G z E y D x
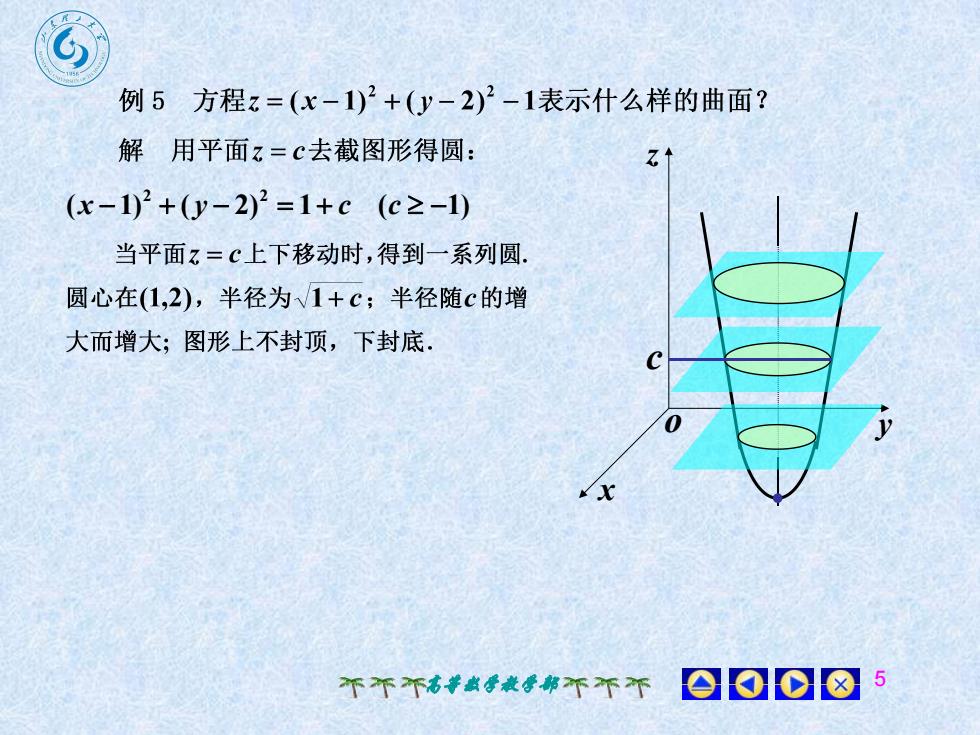
例 5 方程z=(x-1)2+(y-2)2-1表示什么样的曲面?解用平面z=c去截图形得圆:Z(x-1)+(y-2)’=1+c (c≥-1)当平面z=C上下移动时,得到一系列圆圆心在(1,2),半径为~1+c;半径随c的增大而增大;图形上不封顶,下封底108个不不高数学教学部不不个
高等数学教学部 5 ( 1) ( 2) 1 ( 1) 2 2 x y c c z x o y c