《高等数学》课程教学资源（课件讲稿）第九章 多元函数微分学_0907方向导数与梯度

第九章多元函数微分法及其应用第七节方向导数与梯度一、方向导数二、梯度08

第九章 多元函数微分法及其应用 第七节 方向导数与梯度

S引言设函数y= f(x)在点x,的某个邻域内有定义.当自变量 x 在x,处取得增量△r(点x+△r仍在该邻域内），相应地函数取得增量Ay=f(x+△x)-f(x).如果△r→0时△y与△r之比的极限存在，则称之为函数y=f(x)在x,处的导数，并称y=f(x)在x,处可导f(x, +Axr)- f(x,)I(x0)= lim Ay = lim.AxAr-0 AxAr-→0说明导数反映了函数随自变量的变化而变化的快慢程度，导数f'(x）也称为f(x)在x处的变化率0008不不不高数学教学部不不不

高等数学教学部 2 x f x x f x x y f x x x       ( ) ( ) ( ) lim lim 0 0 0 0 0       

S、方向导数1、方向导数的定义1y定义设l是xOy面上以P(xo,J)为始点P(x,y)的一条射线，é, =(cosα,cosβ)是与/同方向的Ayβ单位向量，射线的参数方程为aArP,(xo,yo)[x = X, +tcosα(t ≥ 0).xy = yo + tcosβ0设函数z= f(x,y)在点P,(x,J)的某邻域U(P,)内有定义P(x+tcosα,y.+tcosβ)为l上另一点且 PeU(P） 如果极限f(x, + tcosα,y。+tcos β)-f(xo,Jo)存在，则称此极限为函数lim1-→0+f（x,J）在点P,沿方向l的方向导数，af,- im (x, +tcosa, yo + rcos P)- f(xo yo)2即(xo.Jo)al1→0+001018福个不高教学教学部不不不

高等数学教学部 3 ( 0). cos cos 0 0         t y y t x x t   o y x l P(x, y) x y  ( , ) 0 0 0 P x y t  

Caf方向导数说明就是函数f（x,y）在点P(x,y)沿方向/的all(xo,Jo)变化率。若函数f(x,y）在点P(xo,y)的偏导数存在，且é,=(1,0)，则qaf(xo +1, yo)- f(xo, o) = f. (xo, yo). = limXo.Vt→0+t若函数f(x,）在点P,(xo,y)的偏导数存在，且é,=(0,l)，则aff(xo,J +t)- f(xo, yo) = f,(xo,yo). = limalo.yo1->0+t反之不成立．例如函数z=x2+y2，在点O(0,0)，沿l=i方向,aft-0f(0 +t,0)- f(0,0) = limlim=11(0,0)alt->0+t-→>0+Tt可[Ax / -0f(0 + △x,0) - f(0,0)lim: lim不存在二(0,0)axAxAxAr-→0Ar-→>0001018个不不高等数学教学部不不

高等数学教学部 4 ( , ). ( , ) ( , ) | lim 0 0 0 0 0 0 0 ( , ) 0 0 f x y t f x t y f x y l f x t x y         ( , ). ( , ) ( , ) | lim 0 0 0 0 0 0 0 ( , ) 0 0 f x y t f x y t f x y l f y t x y         1, 0 lim (0 ,0) (0,0) | lim 0 0 (0,0)             t t t f t f l f t t , | | 0 lim (0 ,0) (0,0) | lim 0 0 (0,0) x x x f x f x f x x               

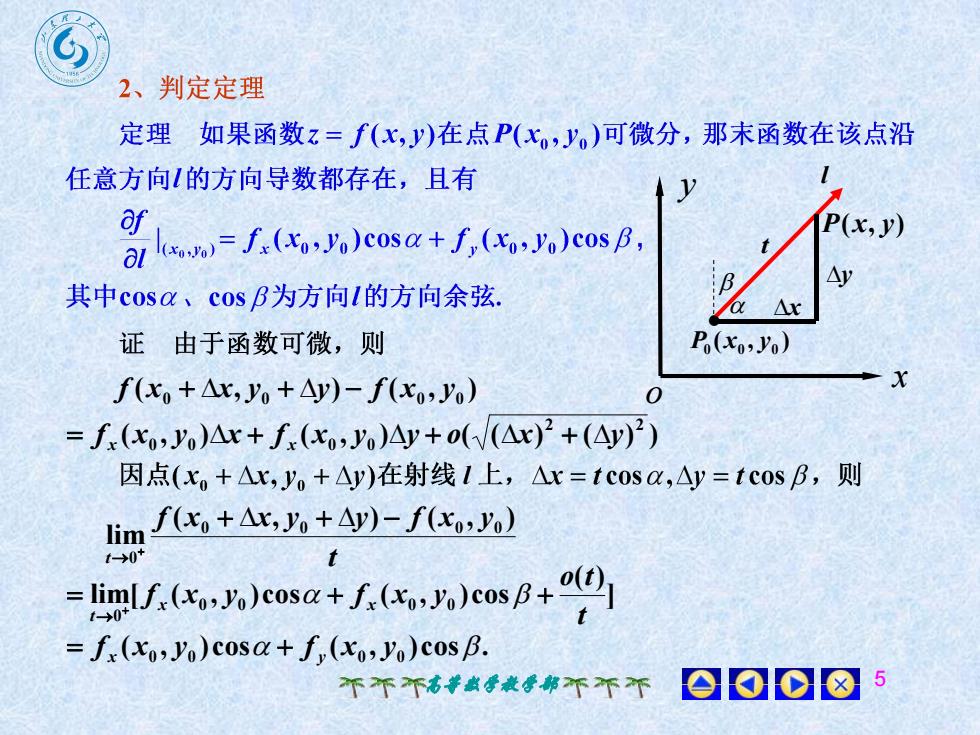
S2、判定定理定理如果函数z= f(x,y)在点 P(x,y)可微分，那末函数在该点沿1任意方向1的方向导数都存在，且有JafP(x,y)al laoo= f.(xo.yo)cosa+ J,(xo, o)cos β.AyB其中cosα、cosβ为方向l的方向余弦AraP.(xo,Jo)证由于函数可微，则xf(x, +Ax, yo +Ay)- f(xo,yo)0= f(xo, yo)Ar + fr(xo,yo)Ay +o(/(Ar)* +(Ay)°)因点(x, +△x,y+Ay)在射线 I 上，△x=tcosα,Ay = tcos β，则f(x + Ax, yo +Ay) - f(xo,yo)lim→0+to(t)= limlf,(xo,yo)cosα + f,(xo,yo)cosβ+= fr(xo,yo)cosα + f,(xo,yo)cos β0008不不不高等数学教学部不不不

高等数学教学部 5 ( , ) ( , ) 0 0 0 0 f x  x y  y  f x y ( , ) ( , ) ( ( ) ( ) ) 2 2 0 0 0 0 f x y x f x y y o x y  x   x      t f x x y y f x y t ( , ) ( , ) lim 0 0 0 0 0        ] ( ) lim[ ( , )cos ( , )cos 0 0 0 0 0 t o t f x y f x y x x t        ( , )cos ( , )cos .  f x x0 y0   f y x0 y0  o y x l P(x, y) x y  ( , ) 0 0 0 P x y t  