《高等数学》课程教学资源（课件讲稿）第十一章 曲线积分与曲面积分_1101对弧长的曲线积分

曲线积分与曲面积分第十一章第一节对弧长的曲线积分对弧长的曲线积分的概念与性质二、对弧长的曲线积分的计算法0

第十一章 曲线积分与曲面积分 第一节 对弧长的曲线积分

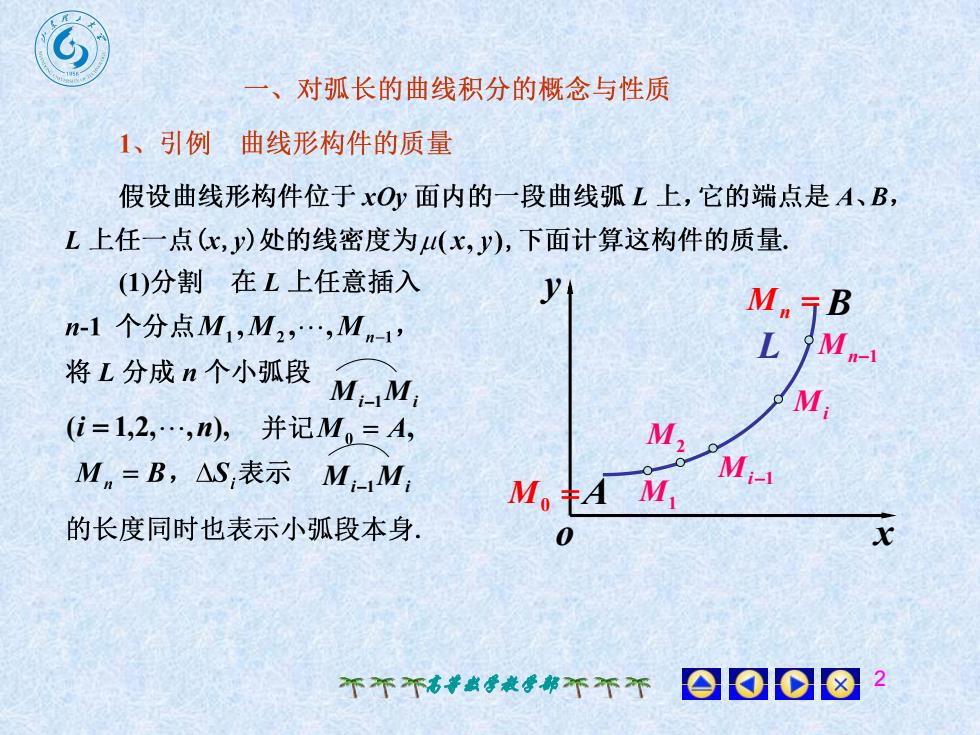
、对弧长的曲线积分的概念与性质1、引例曲线形构件的质量公假设曲线形构件位于xO面内的一段曲线弧 L上，它的端点是A、B,L上任一点(x,y)处的线密度为u(x,y)，下面计算这构件的质量(1)分割 在 L 上任意插入yM,Bn-1 个分点M.,M,,..",M.-1'L Mn-1将L 分成 n 个小弧段M-M,M(i =1,2,...,n), 并记M, = A,MMi-1M,=B，△S,表示Mi-MM.=A M,的长度同时也表示小弧段本身x0o不不个高等数学教学部不不个

高等数学教学部 2 o x y A B Mn1 Mi Mi1 M2 M1 L Mi1Mi (i  1,2,,n), M0  Mn  Mi1Mi

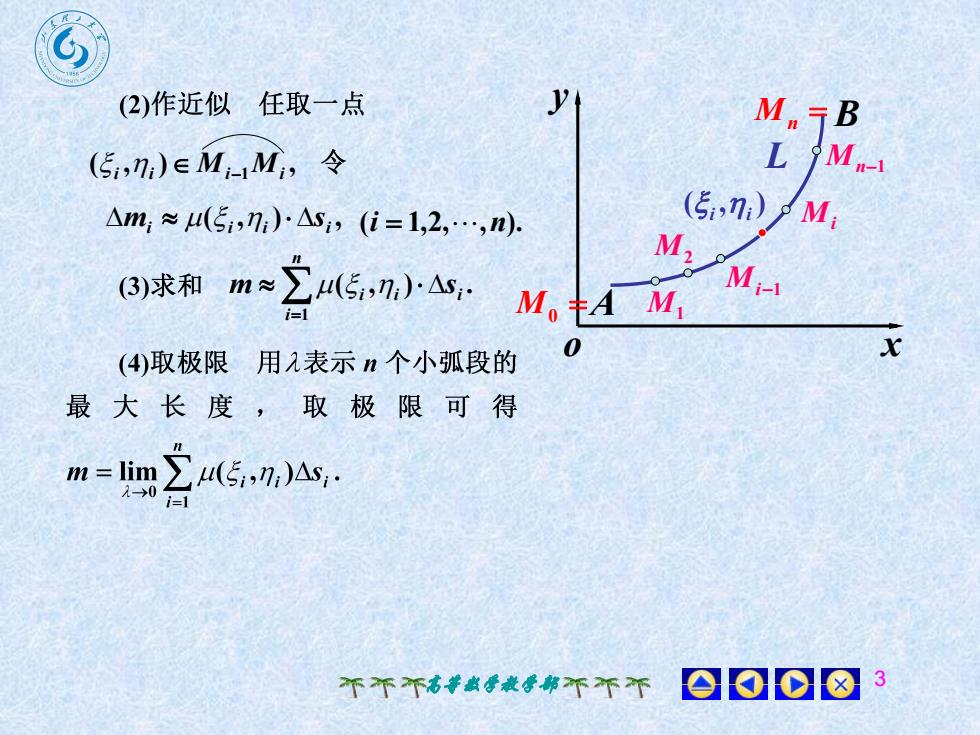
4J(2)作近似 任取一点M,BLM.-1(5i,n,)eM-M, 令(Si,ni)OM,Am, ~ μu(Ei,n.).As,, (i = 1,2,...,n),M2Zu(51,n). As.M.-1(3)求和 m~M,=A M,i=lx0(4)取极限用几表示n个小弧段的最大长度，取极限可得m = lim Zu(5,n,)As,-0i=1008个不不高教学教学部不不不

高等数学教学部 3 o x y A B Mn1 Mi Mi1 M2 M1 L M0  Mn  ( , ) i i  ( , ) ,  i i  Mi1Mi ( , ) , i i i i m      s (i  1,2,,n). ( , ) . 1    n i i i i m    s

福2、对弧长的曲线积分的定义定义设 L为xOy面内的一条光滑曲线弧，函数f(x,y)在L上有界在 L 上任意插入一点列M,M,.,M.，把 L分成 n 个小段.设第 i个小段的长度为△s,，又(,,n)为第i个小段上任意取定的一点，作乘积Zf(5,n;)As 如果当各小段的长度f(5i,n;)△s, (i=1,2,...,n), 并作和i-1的最大值→0时，这和的极限总存在，则称此极限为f(x,J)在曲线弧 L上对弧长的曲线积分或第一类曲线积分，记为J, f(x, )ds = limZ f(5nn,)As,其中f(x,J)叫做被积函数，L 叫做积分弧段以上积分称为第一类曲线积分001018个不高等教学教学部不不不

高等数学教学部 4 ( , ) lim ( , ) . 1  0   n i i i i L f x y ds f   s 

积分存在定理光滑曲线上的连续函数必可积前述曲线形构件的质量为 m=[,u(x,y)ds.推广函数f(x,y,z)在曲线弧「上对弧长的曲线积分J, f(x, y,z)ds = lim Zf(5r,n,5,)As,.001018个不个高等数学教学部不不个

高等数学教学部 5 ( , ) .   L m  x y ds ( , , ) lim ( , , ) . 1 0 i n i i i i f x y z ds f s        